


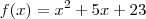 ,completando quadrados ,podemos reescrever
,completando quadrados ,podemos reescrever  como
como 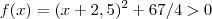 para quaisquer
para quaisquer  .Assim ,é fácil ver que
.Assim ,é fácil ver que 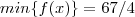 em
em  .Mas ,como
.Mas ,como  inteiro ,calculando
inteiro ,calculando  e
e  ,obtemos
,obtemos 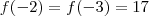 que neste caso , o menor número primo positivo que divide
que neste caso , o menor número primo positivo que divide 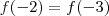 é o próprio 17 .
é o próprio 17 .

 ,será ?Como provar ?
,será ?Como provar ?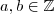 (dependendo de x) tal que
(dependendo de x) tal que 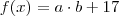 .Se provarmos que de fato existam
.Se provarmos que de fato existam 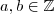 e que o produto deles é par, poderemos concluir que 17 é o menor número primo positivo que divide
e que o produto deles é par, poderemos concluir que 17 é o menor número primo positivo que divide  (Por quê ?).É isto que vamos fazer .
(Por quê ?).É isto que vamos fazer . que é ponto de mínimo de
que é ponto de mínimo de  estar compreendido entre
estar compreendido entre 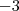 e
e  e
e 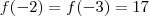 (note que estes valores são raízes da equação
(note que estes valores são raízes da equação 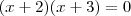 ) .Assim ,tomando-se
) .Assim ,tomando-se 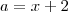 e
e 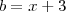 ,segue
,segue 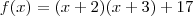 .
. se tomarmos
se tomarmos 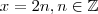 e
e  ,o produto é sempre par (múltiplo de 2)?
,o produto é sempre par (múltiplo de 2)? 


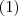 Sabemos
Sabemos 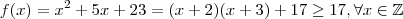
 ,
, 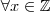 temos sempre
temos sempre  um número par , ou seja ,
um número par , ou seja , 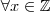 tem-se
tem-se  um número impar.(Verifique !) .
um número impar.(Verifique !) .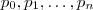 tais que para cada
tais que para cada 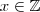 ,
, 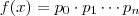 com
com 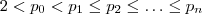 (Observe o item 2) .Assim , definido os números primos ,
(Observe o item 2) .Assim , definido os números primos , 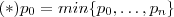 .Agora pelo item (1) ,
.Agora pelo item (1) , 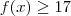 , ou seja ,
, ou seja , 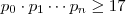 . Logo ,
. Logo , 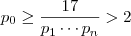 .Vemos então ,
.Vemos então , 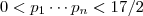 para que
para que 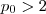 . Mas , o número
. Mas , o número  é impar e diferente que
é impar e diferente que  ,donde obtemos
,donde obtemos 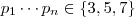 .
. 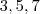 são primos , logo a decomposição
são primos , logo a decomposição  é a trival .Assim ,
é a trival .Assim , 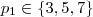 .Se
.Se  ,isto contraria a hipótese
,isto contraria a hipótese  .Caso fosse
.Caso fosse 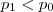 ,
,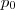 só poderia ser
só poderia ser  pois
pois 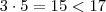 ,logo não existe
,logo não existe 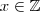 tal que
tal que 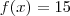 . Caso ,
. Caso , .Segue ,
.Segue , 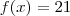 ,mas isto implica
,mas isto implica 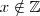 (por favor faça as contas) .Assim , fica evidente que
(por favor faça as contas) .Assim , fica evidente que 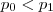 é uma contradição .Para
é uma contradição .Para 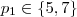 ,segue
,segue  que não é possível determinar
que não é possível determinar 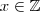 para este caso (Observe as contas acima , basta trocar as letras
para este caso (Observe as contas acima , basta trocar as letras 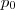 com
com  e manter as estruturas algébricas ) .Assim , só podemos ter a decomposição trivial para
e manter as estruturas algébricas ) .Assim , só podemos ter a decomposição trivial para  .Assim , sendo , segue
.Assim , sendo , segue  logo o menor primo positivo que divide
logo o menor primo positivo que divide  é
é  .
.
 com
com 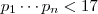 (pois ,se
(pois ,se 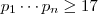 então sempre
então sempre 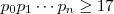 ) .Neste caso ,
) .Neste caso , 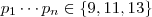 ,logo podemos ter
,logo podemos ter 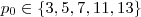 .Além disso,falta analisar o caso em que
.Além disso,falta analisar o caso em que  .Quando estiver disponível tentarei terminar esta questão .
.Quando estiver disponível tentarei terminar esta questão .


 ,observei a função aplicada a estes valores sempre retornou como resposta um número primo .Se conseguimos provar isto(caso fosse verdade) ,ficaria fácil concluir que o menor primo positivo que divide
,observei a função aplicada a estes valores sempre retornou como resposta um número primo .Se conseguimos provar isto(caso fosse verdade) ,ficaria fácil concluir que o menor primo positivo que divide  é o 17 já que o menor valor que a função assume é 17 que para a nossa sorte é primo .
é o 17 já que o menor valor que a função assume é 17 que para a nossa sorte é primo . 

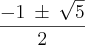 .
.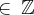 , então o resto r3 , da divisão de n por 3 ,
, então o resto r3 , da divisão de n por 3 , 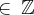 .
.  a afirmação 3 | f(x) também é falsa .
a afirmação 3 | f(x) também é falsa . , pois o gráfico da função é uma parábola .
, pois o gráfico da função é uma parábola .
 o subconjunto do conjunto dos números primos impares.Suponhamos que para cada
o subconjunto do conjunto dos números primos impares.Suponhamos que para cada 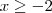 ou
ou  inteiro (pois a função
inteiro (pois a função  não é injetiva ,para cada
não é injetiva ,para cada 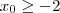 inteiro existe algum
inteiro existe algum 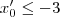 inteiro tal que
inteiro tal que  ) conseguimos números (dependendo de
) conseguimos números (dependendo de  ) primos
) primos 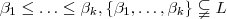 tal que o número composto
tal que o número composto  pode ser reescrito como
pode ser reescrito como 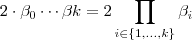 .Assim , sendo
.Assim , sendo 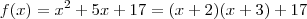 . Segue ,
. Segue , 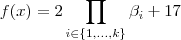 .Além disso ,para cada
.Além disso ,para cada 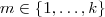 , temos
, temos 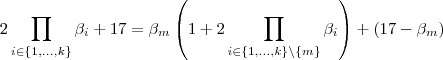 .Ou seja ,
.Ou seja , 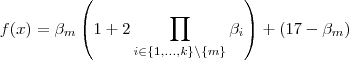 .
. 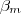 divide
divide  tem-se necessariamente
tem-se necessariamente  (Por quê ? ) .Agora suponhamos
(Por quê ? ) .Agora suponhamos 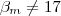 .Pela infinitude dos números primos conseguimos números primos impares distintos dos
.Pela infinitude dos números primos conseguimos números primos impares distintos dos 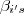 tais que eles dividem f(x).Assim se
tais que eles dividem f(x).Assim se 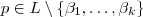 podemos supor que
podemos supor que 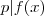 e utilizar o item proposto por você (2) " ...Agora considerando o seguinte teorema : ..." em diante para concluir que
e utilizar o item proposto por você (2) " ...Agora considerando o seguinte teorema : ..." em diante para concluir que  necessariamente é estritamente maior que 17 .
necessariamente é estritamente maior que 17 .
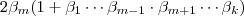 seria
seria 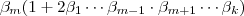 o correto que de forma compacta é :
o correto que de forma compacta é : 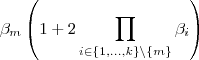 .
.

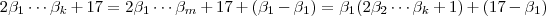 .
. 
 .
.  em
em  temos :
temos : 
 então necessariamente ele é
então necessariamente ele é  . Aparti daí usei o fato da infinidade dos números primos para obtermos números primos que não está na lista (já postada) que divide
. Aparti daí usei o fato da infinidade dos números primos para obtermos números primos que não está na lista (já postada) que divide  e então mostrar que tais números são necessariamente maiores que 17 (usando seu raciocínio) .
e então mostrar que tais números são necessariamente maiores que 17 (usando seu raciocínio) . 
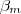 adotar valor = 17 , o valor de x considerado não é ( -2 ) ou (-3) , pois se fosse , o produtório perderia o sentido depois da função ser dividida por
adotar valor = 17 , o valor de x considerado não é ( -2 ) ou (-3) , pois se fosse , o produtório perderia o sentido depois da função ser dividida por 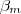 . Certo?
. Certo?



Usuários navegando neste fórum: Nenhum usuário registrado e 8 visitantes
