 por matmatco » Qui Mai 02, 2013 22:43
por matmatco » Qui Mai 02, 2013 22:43
não entendi, para achar os divisores tenho que pegar os multiplos de 2 e 5 é isso?
Sejam os numeros m, n e p com suas respectivas fatoraçoes em primos m =
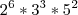
e n=

e p=

nessas condiçoes
quantos divisores de m são multiplos de 100 e quais as condiçoes que devem satisfazer r,s e t para que n seja divisor comum de m e p
Editado pela última vez por
matmatco em Sáb Mai 04, 2013 15:15, em um total de 1 vez.
-
matmatco
- Usuário Parceiro

-
- Mensagens: 60
- Registrado em: Qua Ago 24, 2011 17:32
- Formação Escolar: GRADUAÇÃO
- Área/Curso: matematica UFV
- Andamento: cursando
-
chronoss
- Usuário Dedicado

-
- Mensagens: 34
- Registrado em: Qui Abr 18, 2013 13:59
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por matmatco » Sáb Mai 04, 2013 14:11
por matmatco » Sáb Mai 04, 2013 14:11
obrigado, mas acabei errando na hora de digitar, o 3 é elevado a terceira vou editar
-
matmatco
- Usuário Parceiro

-
- Mensagens: 60
- Registrado em: Qua Ago 24, 2011 17:32
- Formação Escolar: GRADUAÇÃO
- Área/Curso: matematica UFV
- Andamento: cursando
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Aritmética- Duvida em questão do livro praticando aritmética
por wellkirby » Sex Ago 28, 2015 17:37
- 1 Respostas
- 3486 Exibições
- Última mensagem por wellkirby

Seg Set 07, 2015 23:15
Aritmética
-
- [Aritmética] Progressão Aritmética.
por Pessoa Estranha » Qua Ago 28, 2013 22:11
- 2 Respostas
- 5627 Exibições
- Última mensagem por Pessoa Estranha

Qui Ago 29, 2013 16:06
Aritmética
-
- aritmetica
por angeloka » Ter Out 12, 2010 23:52
- 2 Respostas
- 2536 Exibições
- Última mensagem por DanielRJ

Sáb Out 16, 2010 23:16
Álgebra Elementar
-
- Aritmética
por Renatinha » Seg Nov 08, 2010 19:46
- 2 Respostas
- 4972 Exibições
- Última mensagem por Molina

Seg Nov 08, 2010 23:01
Sequências
-
- aritmetica
 por silvia fillet » Qua Out 12, 2011 21:32
por silvia fillet » Qua Out 12, 2011 21:32
- 0 Respostas
- 1345 Exibições
- Última mensagem por silvia fillet

Qua Out 12, 2011 21:32
Álgebra Elementar
Usuários navegando neste fórum: Nenhum usuário registrado e 4 visitantes
Assunto:
Simplifique a expressão com radicais duplos
Autor:
Balanar - Seg Ago 09, 2010 04:01
Simplifique a expressão com radicais duplos abaixo:
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
Resposta:
Dica:
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
(dica : igualar a expressão a

e elevar ao quadrado os dois lados)
Assunto:
Simplifique a expressão com radicais duplos
Autor:
MarceloFantini - Qua Ago 11, 2010 05:46
É só fazer a dica.
Assunto:
Simplifique a expressão com radicais duplos
Autor:
Soprano - Sex Mar 04, 2016 09:49
Olá,
O resultado é igual a 1, certo?
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
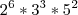 e n=
e n= e p=
e p=  nessas condiçoes
nessas condiçoes
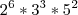 e n=
e n= e p=
e p=  nessas condiçoes
nessas condiçoes
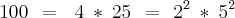

 ; contando você vai chegar a 15 números .
; contando você vai chegar a 15 números .


![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png) (dica : igualar a expressão a
(dica : igualar a expressão a  e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)