 por eliky » Ter Fev 26, 2013 23:49
por eliky » Ter Fev 26, 2013 23:49
Não entendi porque:

Obrigado desde já!
-
eliky
- Usuário Ativo

-
- Mensagens: 14
- Registrado em: Sáb Dez 29, 2012 01:01
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por Russman » Qua Fev 27, 2013 01:08
por Russman » Qua Fev 27, 2013 01:08
Tem certeza que digitou certo a expressão? De onde ela vem? Pois a soma, a princípio, não faz sentido.
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por eliky » Qua Fev 27, 2013 01:34
por eliky » Qua Fev 27, 2013 01:34
A soma destas expressões vêm da cinemática, mas o processo só será algébrico:
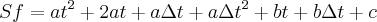
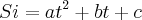
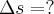
Resposta:

Desculpe não ter colocado anteriormente, e obrigado pela resposta! : D
-
eliky
- Usuário Ativo

-
- Mensagens: 14
- Registrado em: Sáb Dez 29, 2012 01:01
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por Russman » Qua Fev 27, 2013 01:41
por Russman » Qua Fev 27, 2013 01:41
O cálculo da variação está correto. Não entendi sua dúvida, se é que ainda a tenha.
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por eliky » Qua Fev 27, 2013 01:48
por eliky » Qua Fev 27, 2013 01:48
Não entendi como surgiu o
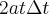
-
eliky
- Usuário Ativo

-
- Mensagens: 14
- Registrado em: Sáb Dez 29, 2012 01:01
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por Russman » Qua Fev 27, 2013 03:20
por Russman » Qua Fev 27, 2013 03:20
A função posição do tempo me parece ser

. Certo?
Você quer calcular a variação de posição entre os instantes

e

. Para isto basta tomar

.
Como

, então

,
de forma que

.
Acredito que você tenha se confundido no desenvolvimento de

, que você chamou de

.
Está claro?
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por eliky » Qua Fev 27, 2013 03:29
por eliky » Qua Fev 27, 2013 03:29
Claríssimo , muito obrigado!!!
-
eliky
- Usuário Ativo

-
- Mensagens: 14
- Registrado em: Sáb Dez 29, 2012 01:01
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Integral da soma/Soma das Integrais.
por Sobreira » Ter Abr 30, 2013 17:41
- 0 Respostas
- 2098 Exibições
- Última mensagem por Sobreira

Ter Abr 30, 2013 17:41
Cálculo: Limites, Derivadas e Integrais
-
- Expressoes
por Biinha » Ter Fev 19, 2013 16:55
- 4 Respostas
- 2438 Exibições
- Última mensagem por Biinha

Sex Fev 22, 2013 11:41
Conjuntos
-
- expressoes
 por Bernardo Silva » Sáb Nov 19, 2016 16:40
por Bernardo Silva » Sáb Nov 19, 2016 16:40
- 1 Respostas
- 1623 Exibições
- Última mensagem por Jadiel Carlos

Seg Nov 21, 2016 11:54
Cálculo: Limites, Derivadas e Integrais
-
- [expressões] ajuda
por kaic » Seg Abr 07, 2008 23:48
- 5 Respostas
- 3979 Exibições
- Última mensagem por admin

Ter Abr 08, 2008 05:04
Álgebra Elementar
-
- [expressões] problema
por Cleyson007 » Ter Jul 01, 2008 01:43
- 9 Respostas
- 16511 Exibições
- Última mensagem por paulo testoni

Qua Out 01, 2008 16:23
Álgebra Elementar
Usuários navegando neste fórum: Nenhum usuário registrado e 7 visitantes
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.





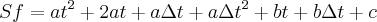
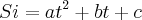
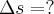



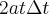

 . Certo?
. Certo? e
e  . Para isto basta tomar
. Para isto basta tomar .
. , então
, então ,
,  .
. , que você chamou de
, que você chamou de  .
.

 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , mas negativo pois tem de ser no quarto quadrante. Se
, mas negativo pois tem de ser no quarto quadrante. Se  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.