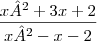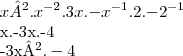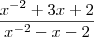Simplificação

AjudaMatematica.com! Aqui você compartilha sua dúvida ou solução!

  • Anúncio Global
    Respostas
    Exibições
    Última mensagem

Simplificação

Regras do fórum
Responder

Simplificação

Mensagempor Rafael Sposito » Dom Fev 17, 2013 13:44

Olá,

Gostaria de saber se essa simplificação está correta, caso não, gentilmente peço que me mostrem a melhor forma de solucionar.

Exercício: Expanda e simplifique as expressão: 3(x+6) 4(2x-5)
3(x+6) 4(2x-5) = 3x+18+8x-20 = 3x+8x + 18-20 = 11x-2

Muito Grato,
Rafael Sposito
Novo Usuário
Novo Usuário
 
Mensagens: 3
Registrado em: Dom Fev 17, 2013 13:35
Formação Escolar: GRADUAÇÃO
Área/Curso: Engenharia
Andamento: cursando
Voltar ao topo

Re: Simplificação

Mensagempor DanielFerreira » Dom Fev 17, 2013 13:58

Olá Rafael,
seja bem-vindo!

Se 3(x + 6) + 4(2x - 4), então, sim! Está correto.
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
DanielFerreira
Colaborador - em formação
Colaborador - em formação
 
Mensagens: 1732
Registrado em: Qui Jul 23, 2009 21:34
Localização: Mangaratiba - RJ
Formação Escolar: GRADUAÇÃO
Área/Curso: Licenciatura em Matemática - IFRJ
Andamento: formado
Voltar ao topo

Re: Simplificação

Mensagempor Rafael Sposito » Dom Fev 17, 2013 16:10

Muito Obrigado...

Poderia me ajudar com essa outra questão de simplificação?!

\frac{x²+3x+2}{x²-x-2}

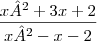
Eu tentei fazer da seguinte forma:

x².{x}^{-2}.3x.{-x}^{-1}.2.{-2}^{-1} x.-3x.-4 -3x².-4

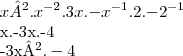
Se estiver errado, eu imagino que possa parecer um meio estranho, mas eu tentei trabalhar com os expoentes. Eu não consegui imaginar uma solução que não fosse essa ou fazer as equações com bascara, que daria um resultado de:

\frac{(-4)+(-5)}{-7}

Muito grato desde já!

PS: Onde estiver um A maisculo, quer dizer um sinal negativo do expoente. Eu coloquei certo no editor, porem apareceu assim aqui. :S
Rafael Sposito
Novo Usuário
Novo Usuário
 
Mensagens: 3
Registrado em: Dom Fev 17, 2013 13:35
Formação Escolar: GRADUAÇÃO
Área/Curso: Engenharia
Andamento: cursando
Voltar ao topo

Re: Simplificação

Mensagempor DanielFerreira » Dom Fev 17, 2013 17:21

Por questões de organização, para cada questão deverás abrir um novo tópico, ok?!

A sua fração é assim?

\frac{x^{- 2}+ 3x + 2}{x^{- 2} - x - 2}

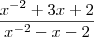
Se for, ela é digitada da seguinte forma:

Código: Selecionar todos
[tex]\frac{x^{- 2}+  3x + 2}{x^{- 2} - x - 2}[/tex]


Até breve!

Daniel.
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
DanielFerreira
Colaborador - em formação
Colaborador - em formação
 
Mensagens: 1732
Registrado em: Qui Jul 23, 2009 21:34
Localização: Mangaratiba - RJ
Formação Escolar: GRADUAÇÃO
Área/Curso: Licenciatura em Matemática - IFRJ
Andamento: formado
Voltar ao topo
Responder

Voltar para Álgebra Elementar

 


Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!

  • Tópicos relacionados
    Respostas
    Exibições
    Última mensagem

Quem está online

Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes

 


Tópico Popular

Assunto: Taxa de variação
Autor: felipe_ad - Ter Jun 29, 2010 19:44

Como resolvo uma questao desse tipo:

Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?

A letra (a) consegui resolver e cheguei no resultado correto de \frac{4\pi{r}^{2}}{3}
Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é 1,066\pi

Alguem me ajuda? Agradeço desde já.

Assunto: Taxa de variação
Autor: Elcioschin - Qua Jun 30, 2010 20:47

V = (1/3)*pi*r²*h ----> h = 4r/3

V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³

Derivando:

dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3

Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s

Assunto: Taxa de variação
Autor: Guill - Ter Fev 21, 2012 21:17

Temos que o volume é dado por:

V = \frac{4\pi}{3}r^2


Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

\frac{dV}{dt} = \frac{8\pi.r}{3}.\frac{dr}{dt}


Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:

\frac{dV}{dt} = \frac{8\pi.2}{3}.\frac{2}{10}

\frac{dV}{dt} = \frac{16\pi}{15}

Powered by phpBB © phpBB Group.

phpBB Mobile / SEO by Artodia.

Índice do fórum