 independe de x, com a e b reais, então a + b vale
independe de x, com a e b reais, então a + b valeA) -4
B) -6
C) -8
D) -10
E) -12
A solução da equação
 é
éA)
![\left[log\frac{1}{10} \right] \left[log\frac{1}{10} \right]](/latexrender/pictures/ef995d0821e8f981e7cb5bbcd76d73c0.png)
B)
![\left[log\frac{1}{20} \right] \left[log\frac{1}{20} \right]](/latexrender/pictures/5f9dfa7381b392da373415e274c9c0b9.png)
C)
![\left[log\frac{1}{30} \right] \left[log\frac{1}{30} \right]](/latexrender/pictures/658aa4e990e1cf774bfb61401fd6a87d.png)
D)
![\left[log\frac{3}{2} \right] \left[log\frac{3}{2} \right]](/latexrender/pictures/34fdc31cc7d05decbc136334f8474b02.png)
E)
![\left[log\frac{2}{3} \right] \left[log\frac{2}{3} \right]](/latexrender/pictures/ff01d25f1a6f58bad35c88bc63782bd9.png)
Se
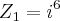 e
e 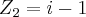 , onde
, onde ![i=\sqrt[]{-1} i=\sqrt[]{-1}](/latexrender/pictures/7dc91cc10f3c198f0d5943cc25d7dc57.png) , então o módulo de
, então o módulo de  é igual a:
é igual a:A)

B)
![\frac{\sqrt[]{2}}{2} \frac{\sqrt[]{2}}{2}](/latexrender/pictures/3e7a67a6d458831b40b1454b389ed266.png)
C)
![\frac{\sqrt[]{3}}{2} \frac{\sqrt[]{3}}{2}](/latexrender/pictures/21682d7c1e802e9b52a99c01850489c4.png)
D)
![\frac{\sqrt[]{3}}{3} \frac{\sqrt[]{3}}{3}](/latexrender/pictures/80dc3f3832b00aa8da65bd3ac29edf6d.png)
E)
![\sqrt[]{3} \sqrt[]{3}](/latexrender/pictures/b84ccc0f808c82dca2d7b0f887c64445.png)
Será que alguem me ajuda por favor........

 independe de x, com a e b reais, então a + b vale
independe de x, com a e b reais, então a + b vale é
é![\left[log\frac{1}{10} \right] \left[log\frac{1}{10} \right]](/latexrender/pictures/ef995d0821e8f981e7cb5bbcd76d73c0.png)
![\left[log\frac{1}{20} \right] \left[log\frac{1}{20} \right]](/latexrender/pictures/5f9dfa7381b392da373415e274c9c0b9.png)
![\left[log\frac{1}{30} \right] \left[log\frac{1}{30} \right]](/latexrender/pictures/658aa4e990e1cf774bfb61401fd6a87d.png)
![\left[log\frac{3}{2} \right] \left[log\frac{3}{2} \right]](/latexrender/pictures/34fdc31cc7d05decbc136334f8474b02.png)
![\left[log\frac{2}{3} \right] \left[log\frac{2}{3} \right]](/latexrender/pictures/ff01d25f1a6f58bad35c88bc63782bd9.png)
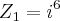 e
e 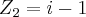 , onde
, onde ![i=\sqrt[]{-1} i=\sqrt[]{-1}](/latexrender/pictures/7dc91cc10f3c198f0d5943cc25d7dc57.png) , então o módulo de
, então o módulo de  é igual a:
é igual a:
![\frac{\sqrt[]{2}}{2} \frac{\sqrt[]{2}}{2}](/latexrender/pictures/3e7a67a6d458831b40b1454b389ed266.png)
![\frac{\sqrt[]{3}}{2} \frac{\sqrt[]{3}}{2}](/latexrender/pictures/21682d7c1e802e9b52a99c01850489c4.png)
![\frac{\sqrt[]{3}}{3} \frac{\sqrt[]{3}}{3}](/latexrender/pictures/80dc3f3832b00aa8da65bd3ac29edf6d.png)
![\sqrt[]{3} \sqrt[]{3}](/latexrender/pictures/b84ccc0f808c82dca2d7b0f887c64445.png)

 , ela é dita "independente de x " quando ela é constante,isto é ,qualquer valor real que
, ela é dita "independente de x " quando ela é constante,isto é ,qualquer valor real que  assumir temos que o resultado de
assumir temos que o resultado de  é o mesmo .
é o mesmo .  .
.  é uma constante real para qualquer
é uma constante real para qualquer  real .
real .  (Claro que (
(Claro que (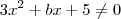 )segue ,
)segue , 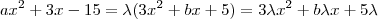 .
. 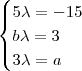 .
.  .
.  deve assumir ?
deve assumir ? 
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante

 .
.
 :
: