 por leonardoandra » Seg Nov 19, 2012 20:44
por leonardoandra » Seg Nov 19, 2012 20:44
Bem, tenho uma equação, da qual eu jah ateh sei o resultadom mas gostaria de saber como foi feito o calculo para chegar no resultado, segue:
equação: 6x^3-4x^2-x-2x^3+2x^2+x
resultado: 4x^3-2x^2
como chegou neste resultado?
obrigado
-
leonardoandra
- Novo Usuário

-
- Mensagens: 5
- Registrado em: Seg Nov 19, 2012 20:34
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Ciencia da Computação
- Andamento: cursando
 por fraol » Seg Nov 19, 2012 21:33
por fraol » Seg Nov 19, 2012 21:33
leonardoandra escreveu:Bem, tenho uma equação, da qual eu jah ateh sei o resultadom mas gostaria de saber como foi feito o calculo para chegar no resultado, segue:
equação: 6x^3-4x^2-x-2x^3+2x^2+x
resultado: 4x^3-2x^2
como chegou neste resultado?
obrigado
Observe:
Partindo de

, vamos agrupar e resolver os termos semelhantes:

= { agrupando, juntando os termos semelhantes, neste caso aqueles contendo

com o mesmo expoente }
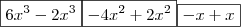
= { resolvendo = somar, subtrair, etc. }

Veja se restou alguma dúvida.
.
-
fraol
- Colaborador Voluntário

-
- Mensagens: 392
- Registrado em: Dom Dez 11, 2011 20:08
- Localização: Mogi das Cruzes-SP
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: formado
 por leonardoandra » Seg Nov 19, 2012 21:48
por leonardoandra » Seg Nov 19, 2012 21:48
Simples neh,
Mto obrigado, eu estava me perdendo no agrupamento, não sabia isso dos termos semelhantes.
Obrigado mesmo!
-
leonardoandra
- Novo Usuário

-
- Mensagens: 5
- Registrado em: Seg Nov 19, 2012 20:34
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Ciencia da Computação
- Andamento: cursando
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Preciso de uma explicação passo a passo para esse exercício
por Dankaerte » Qui Ago 27, 2009 14:24
- 0 Respostas
- 2256 Exibições
- Última mensagem por Dankaerte

Qui Ago 27, 2009 14:24
Sistemas de Equações
-
- Alguém sabe como resolve (5/2)²-5(5/2)+6 passo a passo??
por Elia » Ter Jul 19, 2016 11:28
- 0 Respostas
- 2642 Exibições
- Última mensagem por Elia

Ter Jul 19, 2016 11:28
Sistemas de Equações
-
- Alguém sabe como resolve (5/2)²-5(5/2)+6 passo a passo??
por Elia » Qua Jul 20, 2016 13:57
- 2 Respostas
- 2213 Exibições
- Última mensagem por Elia

Qua Jul 20, 2016 17:51
Equações
-
- [Integração por substituição] Passo a passo, por favor?
por Ronaldobb » Seg Dez 17, 2012 16:24
- 4 Respostas
- 3190 Exibições
- Última mensagem por Ronaldobb

Ter Dez 18, 2012 13:50
Cálculo: Limites, Derivadas e Integrais
-
- Alguém poderia me explicar passo a passo?
por arthurvct » Dom Abr 21, 2013 17:12
- 1 Respostas
- 1476 Exibições
- Última mensagem por ant_dii

Seg Abr 22, 2013 00:31
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Exercicios de polinomios
Autor:
shaft - Qua Jun 30, 2010 17:30

Então, o exercicio pede para encontrar

.
Bom, tentei resolver a questão acima desenvolvendo as duas partes em ( )...Logo dps cheguei em um resultado q nao soube o q fazer mais.
Se vcs puderem ajudar !
Assunto:
Exercicios de polinomios
Autor:
Douglasm - Qua Jun 30, 2010 17:53
Bom, se desenvolvermos isso, encontramos:

Para que os polinômios sejam iguais, seus respectivos coeficientes devem ser iguais (ax = bx ; ax² = bx², etc.):


Somando a primeira e a segunda equação:

Finalmente:

Até a próxima.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



 , vamos agrupar e resolver os termos semelhantes:
, vamos agrupar e resolver os termos semelhantes: = { agrupando, juntando os termos semelhantes, neste caso aqueles contendo
= { agrupando, juntando os termos semelhantes, neste caso aqueles contendo  com o mesmo expoente }
com o mesmo expoente }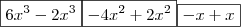 = { resolvendo = somar, subtrair, etc. }
= { resolvendo = somar, subtrair, etc. }



 .
.



