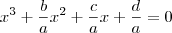
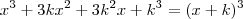
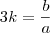
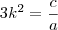
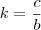


![\sqrt[3]{(x+\frac{c}{b})^3}=\sqrt[3]{-\frac{d}{a}+(\frac{c}{b})^3} \sqrt[3]{(x+\frac{c}{b})^3}=\sqrt[3]{-\frac{d}{a}+(\frac{c}{b})^3}](/latexrender/pictures/288f4affb5ce08b100c717bdb5819051.png)
![x=\sqrt[3]{-\frac{d}{a}+(\frac{c}{b})^3}-\frac{c}{b} x=\sqrt[3]{-\frac{d}{a}+(\frac{c}{b})^3}-\frac{c}{b}](/latexrender/pictures/01dd0d8a1e8527d0b57232d6bb41d1e1.png)
Eu fiz 2x essa dedução e o x ficou isolado dessa maneira mesmo, porém, o resultado não está sendo a raiz da equação cúbica... lamentável, não vejo pq não dá certo... Gostaria duma opinião. Obg!

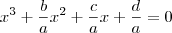
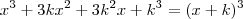
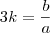
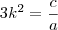
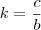


![\sqrt[3]{(x+\frac{c}{b})^3}=\sqrt[3]{-\frac{d}{a}+(\frac{c}{b})^3} \sqrt[3]{(x+\frac{c}{b})^3}=\sqrt[3]{-\frac{d}{a}+(\frac{c}{b})^3}](/latexrender/pictures/288f4affb5ce08b100c717bdb5819051.png)
![x=\sqrt[3]{-\frac{d}{a}+(\frac{c}{b})^3}-\frac{c}{b} x=\sqrt[3]{-\frac{d}{a}+(\frac{c}{b})^3}-\frac{c}{b}](/latexrender/pictures/01dd0d8a1e8527d0b57232d6bb41d1e1.png)

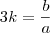
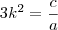


Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png) (dica : igualar a expressão a
(dica : igualar a expressão a  e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)