Aqui vai o primeiro, cuja resposta de acordo com o gabarito é: -15
1 - Considere a equação x² + kx + 36 = 0, na qual x' e x" representam suas raízes. Para que exista a relação
 , o valor de k deverá ser?
, o valor de k deverá ser?Tem que fazer o produto ou algo do tipo?
2 - Certa pessoa entra na igreja e diz a um santo: se você dobrar a quantia de dinheiro que eu tenho, dou-lhe R$ 20.000,00. Dito isso, o santo realizou o milagre e a pessoa, o prometido. Muito animada, ela repetiu a proposta e o santo, o milagre. Feito isso, esta pessoa saiu da igreja sem nenhum dinheiro. Quanto em dinheiro a pessoa possuía ao entrar na igreja?
A resposta de acordo com o gabarito é R$ 15.000,00, mas eu descobri antes pensando pela lógica hehe, pois dobrando essa quantia ficaria 30 mil dando os 20 mil prometidos ficaria com 10 mil, depois dobrando de novo ficaria 20 mil que por fim ela daria como o prometido novamente, saindo sem nada no final. Mas como eu acharia esse resultado com equação?


 e
e  são raízes da equação
são raízes da equação 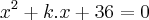 , então:
, então: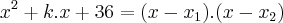

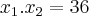

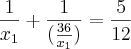 <=>
<=> 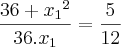
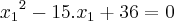



 substitui-se
substitui-se 
 não existem zeros.Senão vejamos
não existem zeros.Senão vejamos

 .Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.