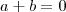. Seja D um domínio e f(x)?D(x). Prove: Se f(x) é divisível por x-a e também por x-b sendo a,b ?D e a?b,então f(x) é divisível por (x-a)(x-b)
Oi eu pensei na divisão da seguinte forma D=d.q+r, como sei que o resto deve ser nulo pois x-a e x-b são divisores de f(x)...comecei dessa forma alguém poderia me ajudar a concluir o racícionío...
f(x)=(x-a).q
f(x)=xq-aq
E
f(x)=(x-b).q
f(x)=xq-bq
Logo xq-aq=xq-bq
-aq=-bq
-aq+bq=0
q(a+b)=0
q=0 ou a+b=0
Muito obrigado


 por
por  dá resto 0, então
dá resto 0, então 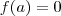
 dá resto 0, então
dá resto 0, então 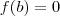
 o quociente e
o quociente e  o resto da divisão do polinômio
o resto da divisão do polinômio  , segue que
, segue que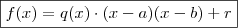
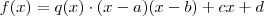
 :
: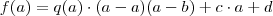
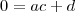
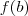 :
: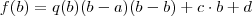
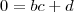
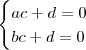
 , mas de acordo com o enunciado,
, mas de acordo com o enunciado, 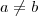 , com isso, podemos concluir que
, com isso, podemos concluir que  . Substituindo esse valor em uma das outras equações, teremos
. Substituindo esse valor em uma das outras equações, teremos 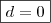 .
.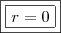
 for o quociente, e tenho certeza que sim, você não pode considerá-lo igual a zero. Mas sim
for o quociente, e tenho certeza que sim, você não pode considerá-lo igual a zero. Mas sim