Estou com dificuldades para resolver essa equação exponencial:
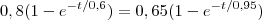
Claramente, t=0 é solução da equação, mas a segunda solução não estou conseguindo obter...
Manipular algebricamente essas exponenciais não é simples. Ou estou mesmo muito enferrujado...
Se alguém puder dar alguma dica de caminho a seguir, agradeceria...


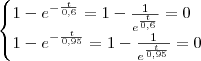

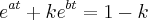 , com a, b e k constantes (E a/b
, com a, b e k constantes (E a/b  2 ou 1/2 - Obrigado Russman!), resolveria meu problema.
2 ou 1/2 - Obrigado Russman!), resolveria meu problema.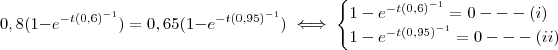
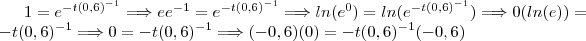 ,
, 
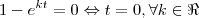
 que vc escreveu, pois não é verdadeiro! (uma vez que a equação tem duas soluções!)
que vc escreveu, pois não é verdadeiro! (uma vez que a equação tem duas soluções!) . Mas poderia não ter, dependendo dos parâmetros envolvidos.
. Mas poderia não ter, dependendo dos parâmetros envolvidos.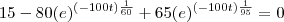 . Agora se fizer
. Agora se fizer 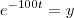 ,achando y logo obterá t ,oque acha ?
,achando y logo obterá t ,oque acha ? 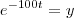 talvez será difícil analiticamente .
talvez será difícil analiticamente .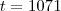 . No entando, fazendo um gráfico, olhando seus pontos de inflexão e seu comportamento no infinito, pude concluir que a única solução real da equação é
. No entando, fazendo um gráfico, olhando seus pontos de inflexão e seu comportamento no infinito, pude concluir que a única solução real da equação é ![\lim_{t\rightarrow\infty}[0,8(1-{e}^{-t/0,6})-0,65(1-{e}^{-t/0,95})] = \lim_{t\rightarrow\infty}[0,8(1-{e}^{-t/0,6})-0,65(1-{e}^{-t/0,95})] =](/latexrender/pictures/256718715b9d969600bcbcd3acffd90b.png)
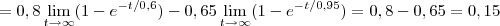
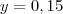 . Portanto, só se anulará em
. Portanto, só se anulará em 
 .
.
 :
: