![\frac{-13- ou + \sqrt[]{133}}{6} \frac{-13- ou + \sqrt[]{133}}{6}](/latexrender/pictures/d52b911106fadd6d63ac599d4de68a27.png) em que q = 3 ou q = 1/3 . Alguma coisa me passou despercebida a respeito da fatoração da raiz de 133...
em que q = 3 ou q = 1/3 . Alguma coisa me passou despercebida a respeito da fatoração da raiz de 133...

![\frac{-13- ou + \sqrt[]{133}}{6} \frac{-13- ou + \sqrt[]{133}}{6}](/latexrender/pictures/d52b911106fadd6d63ac599d4de68a27.png) em que q = 3 ou q = 1/3 . Alguma coisa me passou despercebida a respeito da fatoração da raiz de 133...
em que q = 3 ou q = 1/3 . Alguma coisa me passou despercebida a respeito da fatoração da raiz de 133...

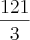 e seu produto é 243.
e seu produto é 243. 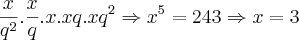 'considerem os . como multiplicações'.
'considerem os . como multiplicações'. 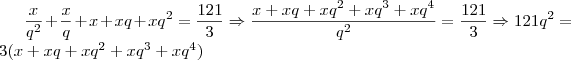
 OU q =
OU q = ![\frac{-13-ou+\sqrt[2]{133}}{6} \frac{-13-ou+\sqrt[2]{133}}{6}](/latexrender/pictures/9332baacc6234c1765cfcdf78aa5b319.png) . Meu erro foi, ao conferir o gabarito, não perceber que estava escrito no mesmo: q = tanto OU tanto OU tanto. Eu entendi que era q = tanto que dará tanto ou tanto. Erro de leitura. De qualquer forma, se alguém aí precisar de algo mais simples, a nível de ens médio que eu puder ajudar. xD
. Meu erro foi, ao conferir o gabarito, não perceber que estava escrito no mesmo: q = tanto OU tanto OU tanto. Eu entendi que era q = tanto que dará tanto ou tanto. Erro de leitura. De qualquer forma, se alguém aí precisar de algo mais simples, a nível de ens médio que eu puder ajudar. xD

Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante

 .
.



