 por Well » Dom Abr 01, 2012 18:14
por Well » Dom Abr 01, 2012 18:14
Tentei provar por absurdo,porém não conseguir desenvolver a demonstração
A afirmação é esta
Se
a é par e não é quadrado perfeito
![\Rightarrow \sqrt[]{a} \Rightarrow \sqrt[]{a}](/latexrender/pictures/237d4b1ac1f3ac5c9b00292f46d0efdc.png)
é irracional
Obrigado.
-
Well
- Novo Usuário

-
- Mensagens: 8
- Registrado em: Qua Mar 28, 2012 21:22
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por fraol » Dom Abr 01, 2012 23:02
por fraol » Dom Abr 01, 2012 23:02
Boa noite,
Vou apresentar uma prova usando um raciocínio parecido com aquele que usamos quando provamos que

é irracional, vejam se vocês concordam:
Vamos assumir que
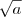
é racional, isto é
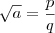
com

e

inteiros positivos,

,

e

primos entre si.
Como

é par, seja
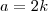
,

um número primo. Então

,
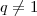
pois

não é quadrado perfeito,
Disso temos
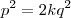
então 2 divide
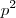
logo 2 divide

.
Assim, seja

, então


Vemos que 2 divide o primeiro membro da equação, então 2 divide o segundo membro também.
2 não divide

, pois assumimos

sendo um número primo. Então 2 deve dividir
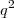
e portanto 2 divide

.
Temos então que 2 é um fator de

e 2 é um fator de

. Dessa forma

e

não são primos entre si, o que contradiz a nossa hipótese.
Logo
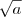
é irracional.
-
fraol
- Colaborador Voluntário

-
- Mensagens: 392
- Registrado em: Dom Dez 11, 2011 20:08
- Localização: Mogi das Cruzes-SP
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: formado
 por fraol » Seg Abr 02, 2012 00:04
por fraol » Seg Abr 02, 2012 00:04
Pessoal,
Apesar de prosaica, quando redigi a prova, ela me parecia tão válida. Porém, relendo agora há pouco vi que tem uma hipótese que não está boa, aquela que supõe a = 2k, k um número primo.
Pois podemos ter, por exemplo, k = 9 que evidentemente não é primo.
Deveríamos considerar k como sendo um conjunto de fatores primos.
Mesmo assim vou pensar mais um pouco.
Sugestões?
-
fraol
- Colaborador Voluntário

-
- Mensagens: 392
- Registrado em: Dom Dez 11, 2011 20:08
- Localização: Mogi das Cruzes-SP
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: formado
 por fraol » Seg Abr 02, 2012 14:42
por fraol » Seg Abr 02, 2012 14:42
Pessoal, quebrando a cabeça, olhando aqui e acolá encontrei uma nova forma de mostrar que a afirmação é verdadeira.
O método, como quase sempre, é por contradição.
Vamos supor que
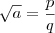
sendo que

é um número racional na forma de fração irredutível e portanto

é mínimo (o menor valor que satisfaz essa igualdade).
Assim

.
Como

é par então
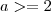
, então
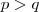
e

senão

seria um quadrado perfeito.
Como

temos

.
Por outro lado,
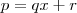
, onde

é o resto da divisão euclidiana,

Se

então

é um quadrado perfeito logo
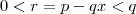
.
Se

então

então
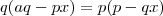
então

.
Como

, temos uma contradição à nossa hipótese de que

é mímimo.
Logo
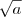
é irracional.
-
fraol
- Colaborador Voluntário

-
- Mensagens: 392
- Registrado em: Dom Dez 11, 2011 20:08
- Localização: Mogi das Cruzes-SP
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: formado
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Logaritmos.( Prove tal afirmação )
por DanielRJ » Qui Out 14, 2010 18:15
- 5 Respostas
- 3764 Exibições
- Última mensagem por MarceloFantini

Sex Out 15, 2010 18:41
Logaritmos
-
- suponha que a # 1 . Mostre que P é verdadeira ...
por abdeco » Seg Mar 30, 2015 12:09
- 0 Respostas
- 1527 Exibições
- Última mensagem por abdeco

Seg Mar 30, 2015 12:09
Álgebra Elementar
-
- Justificar a afirmação
 por silvanuno11 » Sex Mai 25, 2012 12:45
por silvanuno11 » Sex Mai 25, 2012 12:45
- 2 Respostas
- 4112 Exibições
- Última mensagem por silvanuno11

Seg Mai 28, 2012 06:36
Binômio de Newton
-
- Justificar a afirmação
 por silvanuno11 » Dom Mai 27, 2012 16:30
por silvanuno11 » Dom Mai 27, 2012 16:30
- 1 Respostas
- 1625 Exibições
- Última mensagem por PeterHiggs

Qui Mai 31, 2012 11:22
Álgebra Elementar
-
- [Matrizes] Comentar uma afirmação
por fff » Sex Out 10, 2014 07:56
- 0 Respostas
- 2431 Exibições
- Última mensagem por fff

Sex Out 10, 2014 07:56
Matrizes e Determinantes
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Thassya - Sáb Out 01, 2011 16:20
1) Para que os pontos (1,3) e (-3,1) pertençam ao grafico da função f(X)=ax + b ,o valor de b-a deve ser ?
2)Qual o maior valor assumido pela função f : [-7 ,10] em R definida por f(x) = x ao quadrado - 5x + 9?
3) A função f, do primeiro grau, é definida pos f(x)= 3x + k para que o gráfico de f corte o eixo das ordenadas no ponto de ordenada 5 é?
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Neperiano - Sáb Out 01, 2011 19:46
Ola
Qual as suas dúvidas?
O que você não está conseguindo fazer?
Nos mostre para podermos ajudar
Atenciosamente
Assunto:
[Função] do primeiro grau e quadratica
Autor:
joaofonseca - Sáb Out 01, 2011 20:15
1)Dados dois pontos A=(1,3) e B=(-3,1) de uma reta, é possivel definir a sua equação.


Em

substitui-se
m, substitui-se
y e
x por um dos pares ordenados, e resolve-se em ordem a
b.

2)Na equação

não existem zeros.Senão vejamos
Completando o quadrado,

As coordenadas do vertice da parabola são

O eixo de simetria é a reta

.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
f(-7)=93
f(10)=59
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![\Rightarrow \sqrt[]{a} \Rightarrow \sqrt[]{a}](/latexrender/pictures/237d4b1ac1f3ac5c9b00292f46d0efdc.png) é irracional
é irracional
![\Rightarrow \sqrt[]{a} \Rightarrow \sqrt[]{a}](/latexrender/pictures/237d4b1ac1f3ac5c9b00292f46d0efdc.png) é irracional
é irracional
 é irracional, vejam se vocês concordam:
é irracional, vejam se vocês concordam: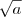 é racional, isto é
é racional, isto é 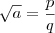
 e
e  inteiros positivos,
inteiros positivos,  ,
,  e
e  primos entre si.
primos entre si. é par, seja
é par, seja 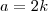 ,
,  um número primo. Então
um número primo. Então ,
, 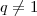 pois
pois  não é quadrado perfeito,
não é quadrado perfeito,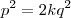 então 2 divide
então 2 divide 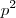 logo 2 divide
logo 2 divide  .
. , então
, então

 , pois assumimos
, pois assumimos  sendo um número primo. Então 2 deve dividir
sendo um número primo. Então 2 deve dividir 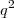 e portanto 2 divide
e portanto 2 divide  .
. e 2 é um fator de
e 2 é um fator de  . Dessa forma
. Dessa forma  e
e  não são primos entre si, o que contradiz a nossa hipótese.
não são primos entre si, o que contradiz a nossa hipótese.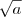 é irracional.
é irracional.

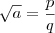 sendo que
sendo que  é um número racional na forma de fração irredutível e portanto
é um número racional na forma de fração irredutível e portanto  é mínimo (o menor valor que satisfaz essa igualdade).
é mínimo (o menor valor que satisfaz essa igualdade). .
. é par então
é par então 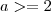 , então
, então 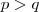 e
e  senão
senão  seria um quadrado perfeito.
seria um quadrado perfeito. temos
temos  .
.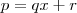 , onde
, onde  é o resto da divisão euclidiana,
é o resto da divisão euclidiana, 
 então
então  é um quadrado perfeito logo
é um quadrado perfeito logo 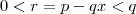 .
. então
então então
então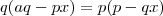 então
então .
. , temos uma contradição à nossa hipótese de que
, temos uma contradição à nossa hipótese de que  é mímimo.
é mímimo.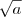 é irracional.
é irracional.


 substitui-se m, substitui-se y e x por um dos pares ordenados, e resolve-se em ordem a b.
substitui-se m, substitui-se y e x por um dos pares ordenados, e resolve-se em ordem a b.
 não existem zeros.Senão vejamos
não existem zeros.Senão vejamos

 .Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.