11 – (Unesp – SP) Considere os pacientes da Aids classificados em três grupos de risco: homofílicos, homossexuais e toxicômanos. Num certo país, de 75 pacientes, verificou – se:
- 41 são homossexuais;
- 9 são homossexuais e hemofílicos, e não são toxicômanos ;
- 7 são homossexuais e toxicômanos, e não são hemofílicos;
- 2 são hemofílicos e toxicômanos, e não são homossexuais;
- 6 pertecem apenas ao grupo de risco dos toxicômanos;
- o número de pacientes que são apenas hemofílicos é igual ao número de pacientes que são apenas homossexuais;
- o número de pacientes que pertencem simultaneamente aos três gruposde risco é a metade do número de pacientes que não pertencem a nenhum dos grupos de risco.
Quantos pacientes pertencem simultaneamente aos três grupos de risco?



 .
.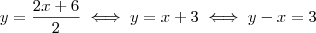 .
. que é a resposta procurada.
que é a resposta procurada.


 .
.
 :
: