 por karkarof » Dom Mar 04, 2012 23:44
por karkarof » Dom Mar 04, 2012 23:44
Olá, estou começando a reaprender matemática, pois fiquei burro. Gostaria da ajuda de vocês neste problema de fatoração, eu até tentei resolver, mas chegou em uma parte que não conseguir continuar.
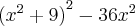
, aí

, E
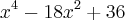
Depois desse eu não conseguir continuar. As alternativas para a resposta são:
A)
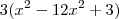
B)
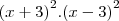
C)
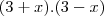
D)
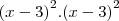
E)

-
karkarof
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Dom Mar 04, 2012 22:45
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Técnico Informática
- Andamento: cursando
 por MarceloFantini » Seg Mar 05, 2012 01:47
por MarceloFantini » Seg Mar 05, 2012 01:47
Faça

, então

. Isto é um trinômio quadrado perfeito, logo
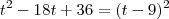
. Mas

, daí
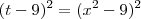
. Lembrando que
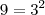
, vemos que

é uma diferença de quadrados. Tente terminar.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por karkarof » Seg Mar 05, 2012 10:42
por karkarof » Seg Mar 05, 2012 10:42
hummm... aff, agora percebi que errei na conta, o correto é:

para finalizar:

=> Diferença de quadrados:

=

=>

=
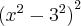
=
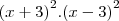
Certo? Letra B.
-
karkarof
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Dom Mar 04, 2012 22:45
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Técnico Informática
- Andamento: cursando
 por MarceloFantini » Seg Mar 05, 2012 13:10
por MarceloFantini » Seg Mar 05, 2012 13:10
O erro também passou despercebido por mim, mas está certo.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Preciso de ajuda em fatoração
 por XxlucasxX » Ter Set 01, 2009 20:29
por XxlucasxX » Ter Set 01, 2009 20:29
- 2 Respostas
- 2078 Exibições
- Última mensagem por Molina

Ter Set 01, 2009 23:21
Álgebra Elementar
-
- Ajuda fatoração algébrica
por lucas7 » Ter Fev 15, 2011 19:53
- 10 Respostas
- 6704 Exibições
- Última mensagem por lucas7

Qui Fev 17, 2011 06:35
Álgebra Elementar
-
- Ajuda em exercício de fatoração
por Luiz Antonio Jr » Qui Mar 03, 2011 12:45
- 7 Respostas
- 3931 Exibições
- Última mensagem por LuizAquino

Qua Mar 23, 2011 10:45
Polinômios
-
- Ajuda com fatoração de polinômios
por samra » Ter Fev 28, 2012 10:01
- 1 Respostas
- 3707 Exibições
- Última mensagem por MarceloFantini

Ter Fev 28, 2012 16:24
Polinômios
-
- [fatoração] fatoração de polinômio do quarto grau.
por +Danilo2 » Qui Set 29, 2016 10:43
- 5 Respostas
- 8917 Exibições
- Última mensagem por +Danilo2

Sáb Out 08, 2016 18:17
Polinômios
Usuários navegando neste fórum: Nenhum usuário registrado e 11 visitantes
Assunto:
Simplifique a expressão com radicais duplos
Autor:
Balanar - Seg Ago 09, 2010 04:01
Simplifique a expressão com radicais duplos abaixo:
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
Resposta:
Dica:
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
(dica : igualar a expressão a

e elevar ao quadrado os dois lados)
Assunto:
Simplifique a expressão com radicais duplos
Autor:
MarceloFantini - Qua Ago 11, 2010 05:46
É só fazer a dica.
Assunto:
Simplifique a expressão com radicais duplos
Autor:
Soprano - Sex Mar 04, 2016 09:49
Olá,
O resultado é igual a 1, certo?
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
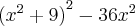 , aí
, aí , E
, E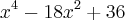
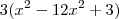
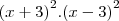
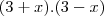
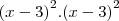


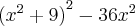 , aí
, aí , E
, E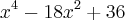
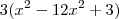
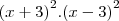
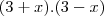
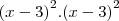


 , então
, então  . Isto é um trinômio quadrado perfeito, logo
. Isto é um trinômio quadrado perfeito, logo 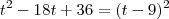 . Mas
. Mas  , daí
, daí 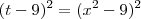 . Lembrando que
. Lembrando que 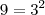 , vemos que
, vemos que  é uma diferença de quadrados. Tente terminar.
é uma diferença de quadrados. Tente terminar.


 => Diferença de quadrados:
=> Diferença de quadrados:  =
=  =>
=>  =
= 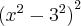 =
= 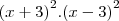


![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png) (dica : igualar a expressão a
(dica : igualar a expressão a  e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)