 por Cleyson007 » Sáb Ago 02, 2008 02:02
por Cleyson007 » Sáb Ago 02, 2008 02:02
Olá boa noite!
Repartindo 420 em três partes que são diretamente proporcionais aos números 3, 7 e 4, respectivamente, encontramos:
a) 90, 210 e 120 b) 90, 300 e 30 c) 60, 240 e 120 d) 60, 220 e 140 e) 90, 200 e 130
No meu modo de pensar, 90 é divisível por 3, 210 por 7 e 120 por 4, está correto o meu pensamento?
Obtive como resposta a alternativa a.
Obrigado.
-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
 por admin » Sáb Ago 02, 2008 21:33
por admin » Sáb Ago 02, 2008 21:33
Olá, boa noite!
Realmente, os três números da resposta terão que ser divisíveis por 3, 7 e 4, respectivamente.
Mas, e se não houvesse altenativa para você testar, como obteria as três partes do resultado?
A propósito, há outras perguntas pendentes em outros tópicos seus.
Bons estudos!
-

admin
- Colaborador Administrador - Professor

-
- Mensagens: 885
- Registrado em: Qui Jul 19, 2007 10:58
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática IME-USP
- Andamento: formado
 por Cleyson007 » Dom Ago 03, 2008 00:49
por Cleyson007 » Dom Ago 03, 2008 00:49
fabiosousa escreveu:Olá, boa noite!
Realmente, os três números da resposta terão que ser divisíveis por 3, 7 e 4, respectivamente.
Mas, e se não houvesse altenativa para você testar, como obteria as três partes do resultado?
A propósito, há outras perguntas pendentes em outros tópicos seus.
Bons estudos!
Olá Fábio Sousa, boa noite!!!
Na medida do possível estarei questionando as dúvidas que ficaram pendentes em outros tópicos.
Pelo que você escreveu parece que a alternativa
a realmente está correta não é?
Até mais.
-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
 por admin » Dom Ago 03, 2008 01:06
por admin » Dom Ago 03, 2008 01:06
Boa noite, Cleyson!
Sim está correta, mas é importante você tentar obter os três números partindo de que você os desconhece.
Pense a partir daqui:
Chamando as três partes procuradas de

,

e

, pela proporcionalidade, há uma constante

tal que:
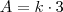
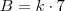
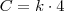
Até mais!
-

admin
- Colaborador Administrador - Professor

-
- Mensagens: 885
- Registrado em: Qui Jul 19, 2007 10:58
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática IME-USP
- Andamento: formado
 por Cleyson007 » Dom Ago 24, 2008 19:20
por Cleyson007 » Dom Ago 24, 2008 19:20
fabiosousa escreveu:Boa noite, Cleyson!
Sim está correta, mas é importante você tentar obter os três números partindo de que você os desconhece.
Pense a partir daqui:
Chamando as três partes procuradas de

,

e

, pela proporcionalidade, há uma constante

tal que:
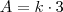
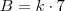
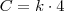
Até mais!
Olá Fabio Sousa, tudo bem contigo?
Consegui perceber pelo que me disse que o valor da constante
K é
30.
Não consegui entender o porque de pensar a partir daqui:
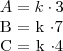
Por favor me explique.
Até mais.
-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
 por admin » Seg Ago 25, 2008 00:38
por admin » Seg Ago 25, 2008 00:38
Cleyson, é a condição de proporcionalidade:
três partes que são diretamente proporcionais aos números 3, 7 e 4, respectivamente
Também podemos escrever assim:
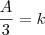
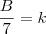
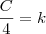
Ser diretamente porporcional como escrito acima, significa que aumentando ou dimimuindo o numerador, o denominador também deve aumentar ou diminuir na mesma proporção, ou seja, os números variam na mesma razão que se mantém constante.
Tendo encontrado o valor da constante de proporcionalidade, substituindo, você terá as três equações com as três partes como incógnitas.
-

admin
- Colaborador Administrador - Professor

-
- Mensagens: 885
- Registrado em: Qui Jul 19, 2007 10:58
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática IME-USP
- Andamento: formado
 por paulo testoni » Qua Out 01, 2008 16:50
por paulo testoni » Qua Out 01, 2008 16:50
Hola Cleyson007.
Fazendo:
3 + 4 + 7 = 14
420 : 14 = 30 é o parâmentro que estamos procurando, então:
30*3 = 90
30*4 = 120
30*7 = 210
-
paulo testoni
- Usuário Dedicado

-
- Mensagens: 45
- Registrado em: Ter Set 30, 2008 11:24
- Formação Escolar: GRADUAÇÃO
- Área/Curso: licenciatura em matemática
- Andamento: formado
 por Cleyson007 » Sáb Mai 30, 2009 13:01
por Cleyson007 » Sáb Mai 30, 2009 13:01
Olá Fábo Sousa e Paulo Testoni!
Entendi o raciocínio da questão

Realmente.. estava testando os valores

Obrigado pela ajuda.
Um abraço
-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Problema
por fabio muniz » Qui Out 23, 2008 16:14
- 1 Respostas
- 10713 Exibições
- Última mensagem por admin

Ter Out 28, 2008 17:47
Problemas do Cotidiano
-
- Problema
por Lima » Dom Dez 14, 2008 18:08
- 3 Respostas
- 9724 Exibições
- Última mensagem por blangis

Dom Dez 14, 2008 20:15
Sistemas de Equações
-
- Problema..
por ANDRE RENATO PROFETA » Sex Mar 13, 2009 00:36
- 1 Respostas
- 3313 Exibições
- Última mensagem por Molina

Sex Mar 13, 2009 14:58
Álgebra Elementar
-
- Problema
por ginrj » Qua Jun 03, 2009 19:19
- 3 Respostas
- 4606 Exibições
- Última mensagem por Cleyson007

Dom Jun 07, 2009 11:48
Álgebra Elementar
-
- Problema. . .
por Fernanda90 » Qui Ago 27, 2009 20:36
- 3 Respostas
- 6528 Exibições
- Última mensagem por Elcioschin

Qui Ago 27, 2009 22:27
Estatística
Usuários navegando neste fórum: Nenhum usuário registrado e 3 visitantes
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.




 ,
,  e
e  , pela proporcionalidade, há uma constante
, pela proporcionalidade, há uma constante  tal que:
tal que: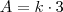
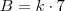
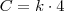
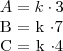
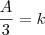
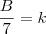
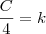


 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.