Esta expressão aparentemente fácil nao deu certo; fiz da seguinte maneira:
Tendo uma diferença de dois quadrados no numerador fatorei e encontrei (x+2)(x-2) restando tb +(x+2)
No denominador conservei (x-1) e fatorei (x²+4x+4)= (x+2)²
Cancelando os termos comuns encontrei
Sendo q a resposta no gabarito é
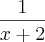
Onde será q eu errei?
Desde já agradeço.
.
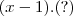, continuando, 
.
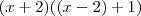
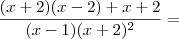
![\frac{(x + 2)[(x - 2) + 1]}{(x - 1)(x + 2)^2} =](/latexrender/pictures/892f66c302c3243c28fc044e09c4f7de.png "\frac{(x + 2)[(x - 2) + 1]}{(x - 1)(x + 2)^2} =")
por ![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png "\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}")
![\sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png "\sqrt[]{2}")
e elevar ao quadrado os dois lados)