Mentes brilhantes de plantão responda-me o porque de (-3)*(-2)=+6;
Só não quero que diga que na multiplicação (-)com (-) é mais .
E o porque de numa divisão de (2/3) / (3/5) tem-se o inverso da segunda fração e não da primeira?



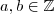 , prove que:
, prove que: 
Neste caso,e
estão limitados ao conjunto dos inteiros, mas a idéia pode ser extendida para outros conjuntos.
 , prove que:
, prove que: 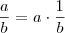
 é um domínio de integridade, este conjunto satisfaz um grupo de axiomas relacionados às operações de soma e produto: propriedade associativa da soma, existência do elemento neutro aditivo, existência do oposto aditivo, comutatividade da soma, associatividade do produto, distributividade à esquerda e à direita, é um anel com unidade, comutativo e não tem divisores de zero.
é um domínio de integridade, este conjunto satisfaz um grupo de axiomas relacionados às operações de soma e produto: propriedade associativa da soma, existência do elemento neutro aditivo, existência do oposto aditivo, comutatividade da soma, associatividade do produto, distributividade à esquerda e à direita, é um anel com unidade, comutativo e não tem divisores de zero. existe um único elemento que chamaremos oposto de
existe um único elemento que chamaremos oposto de  e indicaremos por
e indicaremos por  , tal que
, tal que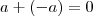
 é o único inteiro que verifica a equação
é o único inteiro que verifica a equação  .
.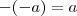
 verifica a equação
verifica a equação  .
. é o oposto de
é o oposto de  que é o elemento indicado por
que é o elemento indicado por 
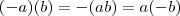
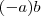 é a solução de
é a solução de  , já que:
, já que:![ab+(-a)b=[(-a)+a]b=0 \cdot b = 0 ab+(-a)b=[(-a)+a]b=0 \cdot b = 0](/latexrender/pictures/db115fa80324be92847383b15992d001.png)
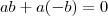 .
.
 .
. e
e  elementos de
elementos de  .
. por
por  será o racional
será o racional  obtido da seguinte forma:
obtido da seguinte forma:
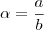 e
e  .
. e
e  números racionais. Então,
números racionais. Então,





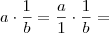
Aplicação da definição de produto:
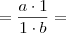
Agora vamos aplicar o axioma da existência da unidade, lembrando que podemos fazer isso poisé domínio de integridade:


Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
 } e B = {
} e B = { }, então o número de elementos A
}, então o número de elementos A  B é:
B é: } você concorda que n só pode ser de 1 a 20? Já que pertence aos naturais?
} você concorda que n só pode ser de 1 a 20? Já que pertence aos naturais? } você concorda que x será os múltiplos de 5 (positivos e negativos)? Já que m pertence ao conjunto Z?
} você concorda que x será os múltiplos de 5 (positivos e negativos)? Já que m pertence ao conjunto Z?sinuca147 escreveu:No processo de determinação dos elementos do conjunto B o que achei foi basicamente os múltiplos de cinco e seus opostos, daí me surgiram estas dúvidas:
existe oposto de zero? sim, é o próprio zero
existe inverso de zero? não, pois não há nenhum número que multiplicado por zero resulte em 1
zero é par, certo? sim, pois pode ser escrito da forma de 2n, onde n pertence aos inteiros
sendo x um número natural, -x é múltiplo de x? Sim, pois basta pegar x e multiplicar por -1 que encontramos -x
sendo z um número inteiro negativo, z é múltiplo de z? Sim, tais perguntando se todo número é multiplo de si mesmo
sendo z um número inteiro negativo, -z é múltiplo de z? Sim, pois basta pegar -z e multiplicar por -1 que encontramos x
A resposta é 3? Sim, pelo menos foi o que vimos a cima

Múltiplo de um número natural é qualquer número que possa ser obtido multiplicando o número natural por 0, 1, 2, 3, 4, 5, etc.
Para determinarmos os múltiplos de 15, por exemplo, devemos multiplicá-lo pela sucessão dos números naturais:
Para determinar os elementos do conjunto A, eu tive de basicamente fazer um lista de vinte dividido por todos os números naturais maiores que zero e menores que vinte e um, finalmente identificando como elementos do conjunto A os números 1, 2, 4, 5, 10 e 20. Acho que procedi de maneira correta, mas fiquei pensando aqui se não existiria um método mais "sofisticado" e prático para que eu pudesse identificar ou ao menos contar o número de elementos do conjunto A, existe?