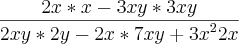por carmem » Ter Mai 12, 2009 23:34
por carmem » Ter Mai 12, 2009 23:34
Me ajudem!
Estou com duvida nestas questões de álgebra elementar:
1) Simplifique:

-
carmem
- Usuário Ativo

-
- Mensagens: 11
- Registrado em: Ter Mai 12, 2009 23:25
- Formação Escolar: SUPLETIVO
- Área/Curso: matematica
- Andamento: cursando
 por Molina » Ter Mai 12, 2009 23:57
por Molina » Ter Mai 12, 2009 23:57
carmem escreveu:Me ajudem!
Estou com duvida nestas questões de álgebra elementar:
1) Simplifique:

Boa noite, Carmem.
Vou tentar primeiramente de dar algumas idéias de como resolver.
Revise a questão de simplicações, todos os modos possíveis.
Tente utilizar talvez de início a colocação de um número em evidência
(os números que são iguais nos monômios).
Caso não tenha nenhum avanço, avise que eu vou postando parte por parte,
ou tudo de uma vez, conforme sua preferência.
Bom estudo!

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por carmem » Qua Mai 13, 2009 11:01
por carmem » Qua Mai 13, 2009 11:01
Bom dia prof. molina, obrigada por responder rapido,tá?
Seria assim? Se não, poderia colocar a resposta para eu ficar tentando?
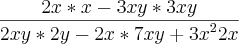
Ou teria outra forma de resolve-la?
Carminha
-
carmem
- Usuário Ativo

-
- Mensagens: 11
- Registrado em: Ter Mai 12, 2009 23:25
- Formação Escolar: SUPLETIVO
- Área/Curso: matematica
- Andamento: cursando
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Simplificação - Ajuda Dúvidas em relação a simplificação
por wgf » Qui Mai 16, 2013 12:56
- 1 Respostas
- 2347 Exibições
- Última mensagem por DanielFerreira

Dom Mai 19, 2013 18:03
Equações
-
- [Simplificação]Fazer a simplificação da resposta
por neoreload » Qua Fev 04, 2015 05:50
- 3 Respostas
- 2863 Exibições
- Última mensagem por neoreload

Sáb Fev 07, 2015 22:10
Equações
-
- [SIMPLIFICAÇÃO] Simplificação expoentes
por brunnkpol » Ter Mai 07, 2013 17:00
- 1 Respostas
- 1827 Exibições
- Última mensagem por DanielFerreira

Sex Mai 10, 2013 00:40
Aritmética
-
- Simplificação
por Jamilly » Qua Mar 17, 2010 21:44
- 1 Respostas
- 2030 Exibições
- Última mensagem por Elcioschin

Qua Mar 17, 2010 22:04
Polinômios
-
- simplificação
por aprendizz » Sáb Mar 27, 2010 16:34
- 2 Respostas
- 1570 Exibições
- Última mensagem por aprendizz

Dom Mar 28, 2010 14:11
Álgebra Elementar
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.