Quais números inteiros positivos menores que 120 podem ser escritos como soma de
duas ou mais potências distintas de base 3 e exponente inteiro maiores do que zero?
DETALHE NÃO SEI POSTAR MINHAS DUVIDAS?



Marlene escreveu:Quais números inteiros positivos menores que 120 podem ser escritos como soma de
duas ou mais potências distintas de base 3 e exponente inteiro maiores do que zero?
 .
. ,
,  ,
,  e
e 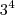 .
.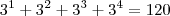 .
.Marlene escreveu:DETALHE NÃO SEI POSTAR MINHAS DUVIDAS?


Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png) (dica : igualar a expressão a
(dica : igualar a expressão a  e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)