 por ninquewylia » Qui Abr 23, 2009 21:13
por ninquewylia » Qui Abr 23, 2009 21:13
Olá a todos, meu primeiro post aqui. Nao sei se postei no lugar correto, caso eu esteja errado, por favor desculpem-me.
Gostaria de saber a resoluçao e resultado de algumas equações que caíram em minha prova, para ver se acertei ou errei.
1.
Um reservatório está totalmente cheio de água. Inicialmente, esvaziou-se  da capacidade desse reservatório e a seguir, retiraram-se 400 litros de água. O volume de água que restou no reservatório após estas operações corresponde a
da capacidade desse reservatório e a seguir, retiraram-se 400 litros de água. O volume de água que restou no reservatório após estas operações corresponde a  da capacidade total do reservatório. Nessas condições, pergunta-se.
da capacidade total do reservatório. Nessas condições, pergunta-se.
a) Quantos litros de água cabem nesse reservatório?
b) Quantos litros de água restam no reservatório?----
2.
Se  , calcule:
, calcule:
a) f(5);
b) f(0);----
3.
Calcule: ![\sqrt[]{4}-\sqrt[3]{27}+\sqrt[4]{16}-\sqrt[5]{-1}. \sqrt[]{4}-\sqrt[3]{27}+\sqrt[4]{16}-\sqrt[5]{-1}.](/latexrender/pictures/5012dd5798d904ed8f9519117e3959d0.png)
----
10.
Determine o valor de x, de modo que os termos (x+3), (4x-2) e (x-1), nessa ordem, formem um P.A----
11.
Fatore:
a) ab-2a-3a+6;
b) 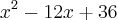
Obs: Só coloquei as questões que tenho dúvidas, eis o motivo de o exercício 3 pular para 10.
Editado pela última vez por
ninquewylia em Qui Abr 23, 2009 21:52, em um total de 1 vez.
-
ninquewylia
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Qui Abr 23, 2009 20:43
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Ensino Médio
- Andamento: cursando
 por rfmswateam » Qui Abr 23, 2009 21:24
por rfmswateam » Qui Abr 23, 2009 21:24
-
rfmswateam
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Qui Abr 23, 2009 21:18
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Estudante
- Andamento: cursando
 por rafagondi » Qui Abr 23, 2009 23:22
por rafagondi » Qui Abr 23, 2009 23:22
________________________________________________
Rafael Agondi - Física/Matemática Bacharelado UNICAMP
-

rafagondi
- Usuário Ativo

-
- Mensagens: 14
- Registrado em: Qui Abr 23, 2009 21:18
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Física Licenciatura - UNICAMP
- Andamento: cursando
 por rafagondi » Qui Abr 23, 2009 23:38
por rafagondi » Qui Abr 23, 2009 23:38
02.
Temos que:

a) Como queremos f(5), temos:
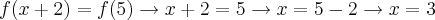
Agora é só aplicar na equação original, substituindo x por 3.
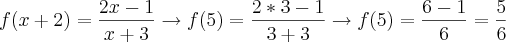
Então:
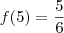
b) Análogamente ao item a), temos:

Aplicando na equação:
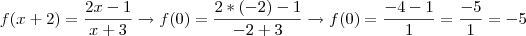
Dessa forma, concluímos que:
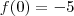
________________________________________________
Rafael Agondi - Física/Matemática Bacharelado UNICAMP
-

rafagondi
- Usuário Ativo

-
- Mensagens: 14
- Registrado em: Qui Abr 23, 2009 21:18
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Física Licenciatura - UNICAMP
- Andamento: cursando
 por rafagondi » Qui Abr 23, 2009 23:46
por rafagondi » Qui Abr 23, 2009 23:46
03.
![\sqrt[]{4}-\sqrt[3]{27}+\sqrt[4]{16}-\sqrt[5]{-1} \sqrt[]{4}-\sqrt[3]{27}+\sqrt[4]{16}-\sqrt[5]{-1}](/latexrender/pictures/9f099a12c9b4d29d5281d9710682de98.png)
![(\sqrt[2]{{2}^{2}})-(\sqrt[3]{{3}^{3}})+(\sqrt[4]{{2}^{4}})-(\sqrt[5]{{(-1)}^{5}}) (\sqrt[2]{{2}^{2}})-(\sqrt[3]{{3}^{3}})+(\sqrt[4]{{2}^{4}})-(\sqrt[5]{{(-1)}^{5}})](/latexrender/pictures/543eb8be29adaea36e3833c5f95cd160.png)
Retirando as raízes, teremos:

Concluímos dessa forma que a solução é 2.
________________________________________________
Rafael Agondi - Física/Matemática Bacharelado UNICAMP
-

rafagondi
- Usuário Ativo

-
- Mensagens: 14
- Registrado em: Qui Abr 23, 2009 21:18
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Física Licenciatura - UNICAMP
- Andamento: cursando
 por rafagondi » Sex Abr 24, 2009 00:04
por rafagondi » Sex Abr 24, 2009 00:04
________________________________________________
Rafael Agondi - Física/Matemática Bacharelado UNICAMP
-

rafagondi
- Usuário Ativo

-
- Mensagens: 14
- Registrado em: Qui Abr 23, 2009 21:18
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Física Licenciatura - UNICAMP
- Andamento: cursando
 por rafagondi » Sex Abr 24, 2009 00:36
por rafagondi » Sex Abr 24, 2009 00:36
11.
a) Não entendi.
b) Temos:
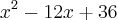
Com um pouco de percepção, percebe-se que esse é um exemplo do quadrado da diferença:
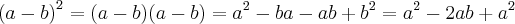
Aplicando-se de forma reversa:
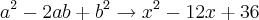

Portanto:

ou

________________________________________________
Rafael Agondi - Física/Matemática Bacharelado UNICAMP
-

rafagondi
- Usuário Ativo

-
- Mensagens: 14
- Registrado em: Qui Abr 23, 2009 21:18
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Física Licenciatura - UNICAMP
- Andamento: cursando
 por Molina » Sex Abr 24, 2009 20:47
por Molina » Sex Abr 24, 2009 20:47
Olá.
Confirme se a 11. a) é isso mesmo que você escreveu.
De qualquer forma, vou fatorar com esses dados que você passou:
11. Fatore:
a) ;
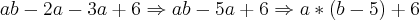
Abraços!

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por rafagondi » Sex Abr 24, 2009 22:44
por rafagondi » Sex Abr 24, 2009 22:44
molina escreveu:Olá.
Confirme se a 11. a) é isso mesmo que você escreveu.
De qualquer forma, vou fatorar com esses dados que você passou:
11. Fatore:
a) ;
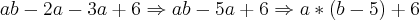
Abraços!

Então, por que ao se "fatorar" dessa forma, o número ainda não resulta em um número que seja um produto; por mais que ele contenha um produto, ele ainda não está na forma fatorada.
________________________________________________
Rafael Agondi - Física/Matemática Bacharelado UNICAMP
-

rafagondi
- Usuário Ativo

-
- Mensagens: 14
- Registrado em: Qui Abr 23, 2009 21:18
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Física Licenciatura - UNICAMP
- Andamento: cursando
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- duvidas de juros simples
por LAURELL3 » Ter Abr 12, 2011 18:44
- 3 Respostas
- 4557 Exibições
- Última mensagem por luizeduardo

Dom Abr 24, 2011 13:18
Matemática Financeira
-
- DUVIDAS JUROS SIMPLES E COMPOSTOS
por DANIEL » Seg Set 01, 2008 17:53
- 3 Respostas
- 6510 Exibições
- Última mensagem por admin

Ter Set 02, 2008 14:41
Matemática Financeira
-
- [Determinantes] Algumas duvidas simples
por fabriel » Seg Jun 03, 2013 00:50
- 2 Respostas
- 3523 Exibições
- Última mensagem por fabriel

Seg Jun 03, 2013 02:52
Álgebra Linear
-
- Duvidas sobre equação trigonométrica simples
por Nana_3000 » Sex Dez 23, 2011 10:09
- 7 Respostas
- 5068 Exibições
- Última mensagem por Nana_3000

Sáb Dez 24, 2011 00:38
Trigonometria
-
- Dúvidas
 por Adriana Barbosa » Seg Jun 01, 2009 11:01
por Adriana Barbosa » Seg Jun 01, 2009 11:01
- 1 Respostas
- 1717 Exibições
- Última mensagem por Molina

Ter Jun 02, 2009 07:00
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
cálculo de limites
Autor:
Hansegon - Seg Ago 25, 2008 11:29
Bom dia.
Preciso de ajuda na solução deste problema, pois só chego ao resultado de 0 sobre 0.
Obrigado
\lim_{x\rightarrow-1} x³ +1/x²-1[/tex]
Assunto:
cálculo de limites
Autor:
Molina - Seg Ago 25, 2008 13:25

Realmente se você jogar o -1 na equação dá 0 sobre 0.
Indeterminações deste tipo você pode resolver por L'Hôpital
que utiliza derivada.
Outro modo é transformar o numerador e/ou denominador
para que não continue dando indeterminado.
Dica: dividir o numerador e o denominador por algum valor é uma forma que normalmente dá certo.

Caso ainda não tenha dado uma

, avisa que eu resolvo.
Bom estudo!
Assunto:
cálculo de limites
Autor:
Guill - Dom Abr 08, 2012 16:03



Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 da capacidade desse reservatório e a seguir, retiraram-se 400 litros de água. O volume de água que restou no reservatório após estas operações corresponde a
da capacidade desse reservatório e a seguir, retiraram-se 400 litros de água. O volume de água que restou no reservatório após estas operações corresponde a  da capacidade total do reservatório. Nessas condições, pergunta-se.
da capacidade total do reservatório. Nessas condições, pergunta-se. , calcule:
, calcule:![\sqrt[]{4}-\sqrt[3]{27}+\sqrt[4]{16}-\sqrt[5]{-1}. \sqrt[]{4}-\sqrt[3]{27}+\sqrt[4]{16}-\sqrt[5]{-1}.](/latexrender/pictures/5012dd5798d904ed8f9519117e3959d0.png)
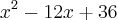




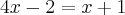



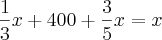
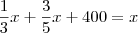



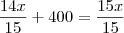
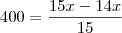
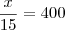





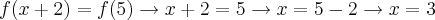
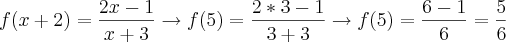
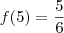

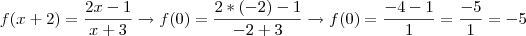
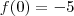
![\sqrt[]{4}-\sqrt[3]{27}+\sqrt[4]{16}-\sqrt[5]{-1} \sqrt[]{4}-\sqrt[3]{27}+\sqrt[4]{16}-\sqrt[5]{-1}](/latexrender/pictures/9f099a12c9b4d29d5281d9710682de98.png)
![(\sqrt[2]{{2}^{2}})-(\sqrt[3]{{3}^{3}})+(\sqrt[4]{{2}^{4}})-(\sqrt[5]{{(-1)}^{5}}) (\sqrt[2]{{2}^{2}})-(\sqrt[3]{{3}^{3}})+(\sqrt[4]{{2}^{4}})-(\sqrt[5]{{(-1)}^{5}})](/latexrender/pictures/543eb8be29adaea36e3833c5f95cd160.png)

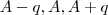

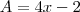



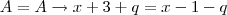
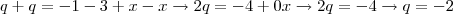



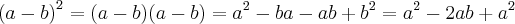
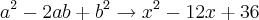

 ou
ou 
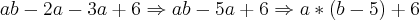



 , avisa que eu resolvo.
, avisa que eu resolvo.

