 por Faria » Sáb Mai 21, 2011 17:43
por Faria » Sáb Mai 21, 2011 17:43
Boa tarde profº, td bem? Eu e meu grupo estamos resolvendo uma lista de exercìcios para
nota. Faltam apenas 4 e, 16 já resovidos. Não temos mais idéia do que fazer. Peço por favor
sua ajuda.
1) Sendo n um número natural, a expressão

é igual a:
Neste exercício tentamos resolver como função exponecial e, também aplicando a distributiva.
2) Se n pertence a N e n>1, então o valor de
![\sqrt[n]{20/{4}^{n+2}+{2}^{2n+2}} \sqrt[n]{20/{4}^{n+2}+{2}^{2n+2}}](/latexrender/pictures/06e08c4cdc0300d6f04b6ad1590f189f.png)
Aqui tentamos resolver o denominador por exponencial e, simplicar o que era possível.
3) O valor de

, para x=111 e
y=112, é:
No exercício em questão tentamos aplicar as regras de fatoração, evidência e simplificação.
4) Calcule o valor de

, sabendo que
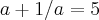
.
No último exercício tentamos calcular o mmc e, depois montamos uma equação do 2º grau,
mas como nos casos anteriores não conseguimos finalizar.
Agradecemos por sua atenção,
Um abraço.
-
Faria
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Sáb Mai 21, 2011 16:49
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: tecnico em processamento de dados
- Andamento: formado
 por MarceloFantini » Sex Set 23, 2011 19:13
por MarceloFantini » Sex Set 23, 2011 19:13
Lembre-se que

,
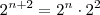
,

,

,
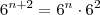
e que podemos fazer
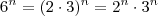
. Tente fazer o primeiro usando isso.
Uma tática quase idêntica se aplica ao segundo, basta lembrar um número com expoente negativo basta inverter a fração, ou seja,

.
Para o terceiro, basta usar que
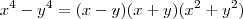
e

.
No último, faça

e veja o que acontece.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- algebra l
por ehrefundini » Qui Mar 05, 2009 08:34
- 1 Respostas
- 7470 Exibições
- Última mensagem por Molina

Qui Mar 05, 2009 21:50
Álgebra
-
- algebra
por uspsilva » Sex Mar 13, 2009 13:03
- 1 Respostas
- 3219 Exibições
- Última mensagem por Molina

Sex Mar 13, 2009 15:22
Pedidos
-
- Algebra
por mattheusramos14 » Ter Ago 03, 2010 01:26
- 1 Respostas
- 2754 Exibições
- Última mensagem por MarceloFantini

Ter Ago 03, 2010 13:37
Álgebra Elementar
-
- ALGEBRA
por JOHNY » Sex Set 03, 2010 23:50
- 1 Respostas
- 2717 Exibições
- Última mensagem por MarceloFantini

Sáb Set 04, 2010 13:12
Álgebra Elementar
-
- álgebra
por Eliana Fidelis » Dom Out 24, 2010 13:52
- 1 Respostas
- 2662 Exibições
- Última mensagem por Adriano Tavares

Ter Mar 08, 2011 20:37
Álgebra Elementar
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de

Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é

Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:

Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:


Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 é igual a:
é igual a:![\sqrt[n]{20/{4}^{n+2}+{2}^{2n+2}} \sqrt[n]{20/{4}^{n+2}+{2}^{2n+2}}](/latexrender/pictures/06e08c4cdc0300d6f04b6ad1590f189f.png)
 , para x=111 e
, para x=111 e  , sabendo que
, sabendo que 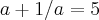 .
.

 ,
, 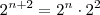 ,
,  ,
,  ,
, 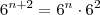 e que podemos fazer
e que podemos fazer 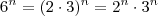 . Tente fazer o primeiro usando isso.
. Tente fazer o primeiro usando isso. .
.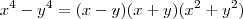 e
e  .
. e veja o que acontece.
e veja o que acontece.






