 por m0x0 » Seg Set 12, 2011 17:36
por m0x0 » Seg Set 12, 2011 17:36
Boas a todos,
Já passei muitas horas de volta deste exercício e não consigo lá chegar. Se alguém me puder ajudar agradecia.
Sejam a,b e c pertencentes aos números naturais e ab, bc e ac cubos perfeitos. Mostrar que a, b e c também são cubos perfeitos.Então, ab é cubo perfeito sse

Passo Base:
P(1):

e

para que

e

P(2):

e

para que

e

Mas também:
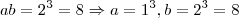
e

para que

e

Ou ainda:
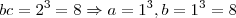
e

para que

e

Passo de Indução:
P(k)=>P(k+1):

E não consigo passar daqui. Não sei como possa provar.. se calhar por indução não é a melhor maneira?
Abraço!
-
m0x0
- Usuário Ativo

-
- Mensagens: 20
- Registrado em: Qui Jul 21, 2011 15:54
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
Usuários navegando neste fórum: Nenhum usuário registrado e 3 visitantes
Assunto:
Exercicios de polinomios
Autor:
shaft - Qua Jun 30, 2010 17:30

Então, o exercicio pede para encontrar

.
Bom, tentei resolver a questão acima desenvolvendo as duas partes em ( )...Logo dps cheguei em um resultado q nao soube o q fazer mais.
Se vcs puderem ajudar !
Assunto:
Exercicios de polinomios
Autor:
Douglasm - Qua Jun 30, 2010 17:53
Bom, se desenvolvermos isso, encontramos:

Para que os polinômios sejam iguais, seus respectivos coeficientes devem ser iguais (ax = bx ; ax² = bx², etc.):


Somando a primeira e a segunda equação:

Finalmente:

Até a próxima.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.

 e
e  para que
para que  e
e 
 e
e  para que
para que  e
e 
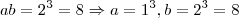 e
e  para que
para que  e
e 
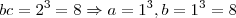 e
e  para que
para que  e
e 




 .
.



