 por LuizCarlos » Seg Ago 15, 2011 14:22
por LuizCarlos » Seg Ago 15, 2011 14:22
Estou tentando resolver um problema de sistema de enquaçãoes com duas incognitas, mas não estou conseguindo entender o problema, interpretar!
A soma das idades de dois jovens é 35 anos. Um deles é 9 anos mais velho que o outro. Calcule a idade de cada um deles.
Comercei fazendo assim:
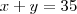
A parte que fala um deles é 9 anos mais velho que o outro, não consegui entender, não consigo equacionar !
-
LuizCarlos
- Colaborador Voluntário

-
- Mensagens: 254
- Registrado em: Ter Jun 21, 2011 20:39
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: 1º ano do segundo grau
- Andamento: cursando
 por Cleyson007 » Seg Ago 15, 2011 16:17
por Cleyson007 » Seg Ago 15, 2011 16:17
Boa tarde Luiz Carlos!
São 02 jovens, sendo eles:
x - Jovem 1 (Jovem mais velho)
y - Jovem 2
x + y = 35 (Primeira condição apresentada no enunciado) I
x = y + 9 (Segunda condição apresentada no enunciado ) II
y + 9 + y = 35
2y = 35 - 9
y = 13 anos
x = 13 + 9
x = 22 anos
Qualquer dúvida é só postar.
Até mais.
-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
 por LuizCarlos » Seg Ago 15, 2011 17:44
por LuizCarlos » Seg Ago 15, 2011 17:44
Cleyson007 escreveu:Boa tarde Luiz Carlos!
São 02 jovens, sendo eles:
x - Jovem 1 (Jovem mais velho)
y - Jovem 2
x + y = 35 (Primeira condição apresentada no enunciado) I
x = y + 9 (Segunda condição apresentada no enunciado ) II
y + 9 + y = 35
2y = 35 - 9
y = 13 anos
x = 13 + 9
x = 22 anos
Qualquer dúvida é só postar.
Até mais.
Ola Cleyson007, eu tou na duvida na parte que fala que um dos jovens é mais velho que o outro !
Da para entender o seguinte, que
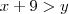
essa idéia de mais velho, confunde!
-
LuizCarlos
- Colaborador Voluntário

-
- Mensagens: 254
- Registrado em: Ter Jun 21, 2011 20:39
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: 1º ano do segundo grau
- Andamento: cursando
 por MarceloFantini » Seg Ago 15, 2011 19:13
por MarceloFantini » Seg Ago 15, 2011 19:13
Alguém ser M anos mais velho que outro quer dizer que a idade de outro é a idade de alguém mais nove.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Problema na resposta de sistema de equações
por chenz » Ter Mai 18, 2010 10:24
- 1 Respostas
- 3319 Exibições
- Última mensagem por chenz

Ter Mai 18, 2010 10:42
Sistemas de Equações
-
- Como montar o sistema de equações deste problema?
por macedo1967 » Qua Set 20, 2017 19:38
- 1 Respostas
- 6611 Exibições
- Última mensagem por DanielFerreira

Sex Set 22, 2017 20:11
Sistemas de Equações
-
- [Sistema Linear] MACK-SP: Sistema de Equações
por ALF » Sex Ago 26, 2011 13:24
- 1 Respostas
- 4487 Exibições
- Última mensagem por LuizAquino

Dom Ago 28, 2011 12:57
Sistemas de Equações
-
- [SISTEMA] problema que envolve um sistema
por brunnkpol » Qui Jan 02, 2014 22:57
- 2 Respostas
- 2704 Exibições
- Última mensagem por brunnkpol

Seg Jan 06, 2014 21:37
Sistemas de Equações
-
- Sistema de equações
por Cleyson007 » Sex Set 12, 2008 12:47
- 6 Respostas
- 5526 Exibições
- Última mensagem por Cleyson007

Qua Jun 03, 2009 17:25
Sistemas de Equações
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
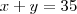



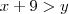


 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.