 por Joan » Seg Jul 25, 2011 16:38
por Joan » Seg Jul 25, 2011 16:38
Sejam p e q números reais positicos tais que
![\frac{1}{p} + \frac{1}{q} = \frac{1}{\sqrt[]{2010}} \frac{1}{p} + \frac{1}{q} = \frac{1}{\sqrt[]{2010}}](/latexrender/pictures/16c434558b78f2ff3ae8e62e1027459f.png)
. Qual o valor mínimo do produto pq?
oq consegui fazer foi somente o inicio e depois nao sei oq faço:
![\frac{p+q}{pq} = \frac{1}{\sqrt[]{2010}} \rightarrow p+q = \frac{pq}{\sqrt[]{2010}} \frac{p+q}{pq} = \frac{1}{\sqrt[]{2010}} \rightarrow p+q = \frac{pq}{\sqrt[]{2010}}](/latexrender/pictures/0da559bb010c5e1b7ac55e8304d37fda.png)
Infelismente nao sei oq fazer mais...
desde já grato.
-
Joan
- Usuário Ativo

-
- Mensagens: 12
- Registrado em: Sex Jul 22, 2011 18:07
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por Joan » Seg Jul 25, 2011 18:04
por Joan » Seg Jul 25, 2011 18:04
Amigo agradeço a boa vontade, mais no gabarito da prova tá a resposta como 8040. oq pode ta errado?
-
Joan
- Usuário Ativo

-
- Mensagens: 12
- Registrado em: Sex Jul 22, 2011 18:07
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por MarceloFantini » Ter Jul 26, 2011 11:04
por MarceloFantini » Ter Jul 26, 2011 11:04
Continuando o que o colega Guill fez, temos:

Mas sabemos que

. Portanto,
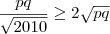
e segue que
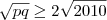
. Finalmente,

, e a resposta é que o valor mínimo de
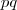
é 8040.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por LuizAquino » Ter Jul 26, 2011 11:25
por LuizAquino » Ter Jul 26, 2011 11:25
Guill escreveu:Racionalizando:
![\frac{p+q}{pq}=\frac{\sqrt[]{2010}}{2010} \frac{p+q}{pq}=\frac{\sqrt[]{2010}}{2010}](/latexrender/pictures/b3d4c370b9f2f07c13b0693d43fc7c2e.png)
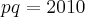
Joan escreveu:Amigo agradeço a boa vontade, mais no gabarito da prova tá a resposta como 8040. oq pode ta errado?
O erro na solução de Guill está no fato de que se
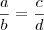
, então
não necessariamente a = c e b = d.
Por exemplo, se a = 5 e b = 10, temos que
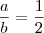
. Entretanto, note que
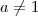
e
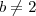
.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por Joan » Ter Jul 26, 2011 14:55
por Joan » Ter Jul 26, 2011 14:55
Nao comprendi, mais obrigado a todos pela ajuda.
-
Joan
- Usuário Ativo

-
- Mensagens: 12
- Registrado em: Sex Jul 22, 2011 18:07
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por Fabricio dalla » Ter Jul 26, 2011 16:47
por Fabricio dalla » Ter Jul 26, 2011 16:47
Mas sabemos que
![\frac{p+q}{2}\geq\sqrt[2]{pq} \frac{p+q}{2}\geq\sqrt[2]{pq}](/latexrender/pictures/f431ac8ae5c2163d1397860bc2668184.png)
eu n entendi o que Marcelo Fantine fez.ele pré supôs fazendo aquela comparaçao de que a media aritimetica e maior que media geometrica pra conseguir resolver a questão ?
-
Fabricio dalla
- Colaborador Voluntário

-
- Mensagens: 111
- Registrado em: Sáb Fev 26, 2011 17:50
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por MarceloFantini » Ter Jul 26, 2011 16:58
por MarceloFantini » Ter Jul 26, 2011 16:58
Isso é um teorema importante, que a média aritmética é sempre maior ou igual a média geométrica.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por LuizAquino » Ter Jul 26, 2011 21:35
por LuizAquino » Ter Jul 26, 2011 21:35
Fabricio dalla escreveu:eu n entendi o que Marcelo Fantine fez.ele pré supôs fazendo aquela comparaçao de que a media aritimetica e maior que media geometrica pra conseguir resolver a questão ?
Dados dois números reais positivos, é fácil verificar que

.
Em outras palavras, como escreveu o colega Fantini, essa desigualdade nos diz que
a média aritmética entre dois números é sempre maior ou igual do que a média geométrica entre eles.
Para justificar essa desigualdade, começamos observando o fato de que
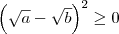
, para quaisquer
a e
b reais positivos.
Desenvolvendo o produto notável, obtemos:

Mas, isso é o mesmo que:
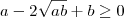
Por fim, podemos reescrever essa desigualdade como:

#
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- MMC e MDC - Colégio Naval
por igorcamilo » Sáb Jun 25, 2011 21:22
- 1 Respostas
- 2028 Exibições
- Última mensagem por FilipeCaceres

Dom Jun 26, 2011 16:13
Álgebra Elementar
-
- Divisibilidade - Colégio naval
por igorcamilo » Sex Jun 24, 2011 19:22
- 2 Respostas
- 2459 Exibições
- Última mensagem por igorcamilo

Sex Jun 24, 2011 20:32
Álgebra Elementar
-
- Colégio Naval - Aritmética dos inteiros
por eliky » Sex Mai 17, 2013 01:16
- 1 Respostas
- 2330 Exibições
- Última mensagem por DanielFerreira

Dom Mai 19, 2013 20:40
Aritmética
-
- [triângulo equilátero] Questão Colégio Naval 2010
 por Joan » Sex Jul 22, 2011 18:42
por Joan » Sex Jul 22, 2011 18:42
- 3 Respostas
- 3717 Exibições
- Última mensagem por Joan

Sáb Jul 23, 2011 11:34
Geometria Plana
-
- [conjunto solução em R] Questão Colégio Naval 2010
por Joan » Sáb Jul 23, 2011 12:06
- 2 Respostas
- 5385 Exibições
- Última mensagem por Joan

Sáb Jul 23, 2011 13:21
Equações
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
(FGV) ... função novamente rs
Autor:
my2009 - Qua Dez 08, 2010 21:48
Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
Assunto:
(FGV) ... função novamente rs
Autor: Anonymous - Qui Dez 09, 2010 17:25
Uma função de 1º grau é dada por

.
Temos que para

,

e para

,

.

Ache o valor de

e

, monte a função e substitua

por

.
Assunto:
(FGV) ... função novamente rs
Autor:
Pinho - Qui Dez 16, 2010 13:57
my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
f(x)= 2.x
f(3)=2.3=6
f(4)=2.4=8
f(10)=2.10=20
Assunto:
(FGV) ... função novamente rs
Autor:
dagoth - Sex Dez 17, 2010 11:55
isso ai foi uma questao da FGV?
haahua to precisando trocar de faculdade.
Assunto:
(FGV) ... função novamente rs
Autor:
Thiago 86 - Qua Mar 06, 2013 23:11
Saudações!

ví suaquestão e tentei resolver, depois você conta-me se eu acertei.
Uma função de 1º grau é dada por y=3a+b
Resposta :
3a+b=6 x(4)
4a+b=8 x(-3)
12a+4b=24
-12a-3b=-24
b=0
substituindo b na 1°, ttenho que: 3a+b=6
3a+0=6
a=2
substituindo em: y=3a+b
y=30+0
y=30

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![\frac{1}{p} + \frac{1}{q} = \frac{1}{\sqrt[]{2010}} \frac{1}{p} + \frac{1}{q} = \frac{1}{\sqrt[]{2010}}](/latexrender/pictures/16c434558b78f2ff3ae8e62e1027459f.png) . Qual o valor mínimo do produto pq?
. Qual o valor mínimo do produto pq?![\frac{p+q}{pq} = \frac{1}{\sqrt[]{2010}} \rightarrow p+q = \frac{pq}{\sqrt[]{2010}} \frac{p+q}{pq} = \frac{1}{\sqrt[]{2010}} \rightarrow p+q = \frac{pq}{\sqrt[]{2010}}](/latexrender/pictures/0da559bb010c5e1b7ac55e8304d37fda.png)

![\frac{1}{p} + \frac{1}{q} = \frac{1}{\sqrt[]{2010}} \frac{1}{p} + \frac{1}{q} = \frac{1}{\sqrt[]{2010}}](/latexrender/pictures/16c434558b78f2ff3ae8e62e1027459f.png) . Qual o valor mínimo do produto pq?
. Qual o valor mínimo do produto pq?![\frac{p+q}{pq} = \frac{1}{\sqrt[]{2010}} \rightarrow p+q = \frac{pq}{\sqrt[]{2010}} \frac{p+q}{pq} = \frac{1}{\sqrt[]{2010}} \rightarrow p+q = \frac{pq}{\sqrt[]{2010}}](/latexrender/pictures/0da559bb010c5e1b7ac55e8304d37fda.png)

![\frac{1}{p}+\frac{1}{q}=\frac{1}{\sqrt[]{2010}} \frac{1}{p}+\frac{1}{q}=\frac{1}{\sqrt[]{2010}}](/latexrender/pictures/ff0b452167f0b238afbe83cc525d56ee.png)
![\frac{p+q}{pq}=\frac{1}{\sqrt[]{2010}} \frac{p+q}{pq}=\frac{1}{\sqrt[]{2010}}](/latexrender/pictures/96ff4eea56ba5117aeeda02f3618b376.png)
![\frac{p+q}{pq}=\frac{\sqrt[]{2010}}{2010} \frac{p+q}{pq}=\frac{\sqrt[]{2010}}{2010}](/latexrender/pictures/b3d4c370b9f2f07c13b0693d43fc7c2e.png)
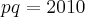



 . Portanto,
. Portanto, 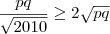 e segue que
e segue que 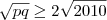 . Finalmente,
. Finalmente,  , e a resposta é que o valor mínimo de
, e a resposta é que o valor mínimo de 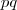 é 8040.
é 8040.

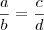 , então não necessariamente a = c e b = d.
, então não necessariamente a = c e b = d.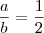 . Entretanto, note que
. Entretanto, note que 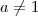 e
e 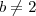 .
.

![\frac{p+q}{2}\geq\sqrt[2]{pq} \frac{p+q}{2}\geq\sqrt[2]{pq}](/latexrender/pictures/f431ac8ae5c2163d1397860bc2668184.png)



 .
.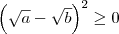 , para quaisquer a e b reais positivos.
, para quaisquer a e b reais positivos.
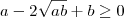


 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
