 por theSinister » Sex Jun 17, 2011 18:42
por theSinister » Sex Jun 17, 2011 18:42
-
theSinister
- Usuário Dedicado

-
- Mensagens: 41
- Registrado em: Sáb Abr 23, 2011 18:36
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por tcgm » Sex Jun 17, 2011 23:04
por tcgm » Sex Jun 17, 2011 23:04
Não desmembre a raiz quando dentro dela houver uma soma ou subtração.
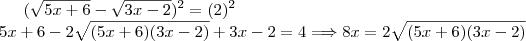
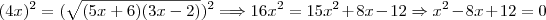
Passando a equação pra forma canônica:
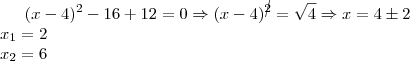
TM

-
tcgm
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Sex Jun 17, 2011 22:51
- Formação Escolar: ENSINO FUNDAMENTAL II
- Área/Curso: Eletrônica
- Andamento: cursando
 por theSinister » Sex Jun 17, 2011 23:45
por theSinister » Sex Jun 17, 2011 23:45
ainda não consegui entender cara, tipo vc elevou os dois membros ao quadrado certo? ai pq o 5x+6 saiu da raiz?
-
theSinister
- Usuário Dedicado

-
- Mensagens: 41
- Registrado em: Sáb Abr 23, 2011 18:36
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por tcgm » Sáb Jun 18, 2011 23:00
por tcgm » Sáb Jun 18, 2011 23:00
Você sabe produtos notáveis? Se souber, sabe também que:
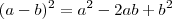
Aplicando isso no problema:
![(\sqrt{5x+6}-\sqrt{3x-2})^2=[(\sqrt{5x+6})^2-2\sqrt{(5x+6)(3x-2)}+(\sqrt{3x-2})^2] (\sqrt{5x+6}-\sqrt{3x-2})^2=[(\sqrt{5x+6})^2-2\sqrt{(5x+6)(3x-2)}+(\sqrt{3x-2})^2]](/latexrender/pictures/eb56b654469ce569bca8788366c1f51b.png)
Resolvendo isso fica:

TM

-
tcgm
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Sex Jun 17, 2011 22:51
- Formação Escolar: ENSINO FUNDAMENTAL II
- Área/Curso: Eletrônica
- Andamento: cursando
 por theSinister » Sáb Jun 18, 2011 23:49
por theSinister » Sáb Jun 18, 2011 23:49
vlw cara, agora eu entendi.
-
theSinister
- Usuário Dedicado

-
- Mensagens: 41
- Registrado em: Sáb Abr 23, 2011 18:36
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- simplificar expressões com radicais
por theSinister » Dom Jun 12, 2011 19:17
- 8 Respostas
- 8775 Exibições
- Última mensagem por theSinister

Seg Jun 13, 2011 15:10
Álgebra Elementar
-
- LIMITE COM RADICAIS como fatorar ou simplificar
por pedroklein+1978 » Ter Abr 25, 2017 18:42
- 0 Respostas
- 2867 Exibições
- Última mensagem por pedroklein+1978

Ter Abr 25, 2017 18:42
Cálculo: Limites, Derivadas e Integrais
-
- Simplificar
por Sandy26 » Ter Abr 27, 2010 14:35
- 5 Respostas
- 3183 Exibições
- Última mensagem por MarceloFantini

Qui Abr 29, 2010 18:29
Cálculo: Limites, Derivadas e Integrais
-
- Radicais
por agfp5 » Sáb Out 30, 2010 08:50
- 2 Respostas
- 2335 Exibições
- Última mensagem por agfp5

Sáb Out 30, 2010 09:10
Geometria Plana
-
- Simplificar
por victorleme » Qua Mai 04, 2011 20:06
- 4 Respostas
- 2522 Exibições
- Última mensagem por victorleme

Qui Mai 05, 2011 18:56
Polinômios
Usuários navegando neste fórum: Nenhum usuário registrado e 13 visitantes
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![\sqrt[2]{5x+6}-\sqrt[2]{3x-2}=2 \sqrt[2]{5x+6}-\sqrt[2]{3x-2}=2](/latexrender/pictures/ce27b6e909c652219a55fc86f088e145.png)
![\sqrt[]{5x}+\sqrt[]{2.3}-\sqrt[]{3x}.\sqrt[]{-2}=2 \sqrt[]{5x}+\sqrt[]{2.3}-\sqrt[]{3x}.\sqrt[]{-2}=2](/latexrender/pictures/85584d71506e5e013e792a19096eb0c1.png)
![\sqrt[]{5x}+\sqrt[]{2}.\sqrt[]{3}-\sqrt[]{3x}.\sqrt[]{-2}=2 \sqrt[]{5x}+\sqrt[]{2}.\sqrt[]{3}-\sqrt[]{3x}.\sqrt[]{-2}=2](/latexrender/pictures/b85627bee7e9114ccd0e77827c13e851.png)
![\sqrt[]{5x}+(-2).\sqrt[]{3}-\sqrt[]{3x}=2 \sqrt[]{5x}+(-2).\sqrt[]{3}-\sqrt[]{3x}=2](/latexrender/pictures/af100d92c6c65475ef03b80e75d44d7f.png)
![\sqrt[]{5x}+(-2).3x=2 \sqrt[]{5x}+(-2).3x=2](/latexrender/pictures/4555cb3a2c068518db8f96010d1f5246.png)
![\sqrt[]{5x}-6x=2 \sqrt[]{5x}-6x=2](/latexrender/pictures/6963e149a3e2f76b46498c32b7a23a3d.png)

![\sqrt[2]{5x+6}-\sqrt[2]{3x-2}=2 \sqrt[2]{5x+6}-\sqrt[2]{3x-2}=2](/latexrender/pictures/ce27b6e909c652219a55fc86f088e145.png)
![\sqrt[]{5x}+\sqrt[]{2.3}-\sqrt[]{3x}.\sqrt[]{-2}=2 \sqrt[]{5x}+\sqrt[]{2.3}-\sqrt[]{3x}.\sqrt[]{-2}=2](/latexrender/pictures/85584d71506e5e013e792a19096eb0c1.png)
![\sqrt[]{5x}+\sqrt[]{2}.\sqrt[]{3}-\sqrt[]{3x}.\sqrt[]{-2}=2 \sqrt[]{5x}+\sqrt[]{2}.\sqrt[]{3}-\sqrt[]{3x}.\sqrt[]{-2}=2](/latexrender/pictures/b85627bee7e9114ccd0e77827c13e851.png)
![\sqrt[]{5x}+(-2).\sqrt[]{3}-\sqrt[]{3x}=2 \sqrt[]{5x}+(-2).\sqrt[]{3}-\sqrt[]{3x}=2](/latexrender/pictures/af100d92c6c65475ef03b80e75d44d7f.png)
![\sqrt[]{5x}+(-2).3x=2 \sqrt[]{5x}+(-2).3x=2](/latexrender/pictures/4555cb3a2c068518db8f96010d1f5246.png)
![\sqrt[]{5x}-6x=2 \sqrt[]{5x}-6x=2](/latexrender/pictures/6963e149a3e2f76b46498c32b7a23a3d.png)

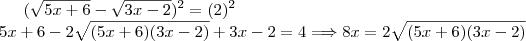
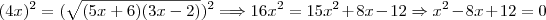
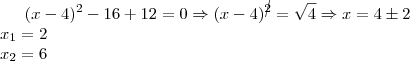


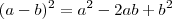
![(\sqrt{5x+6}-\sqrt{3x-2})^2=[(\sqrt{5x+6})^2-2\sqrt{(5x+6)(3x-2)}+(\sqrt{3x-2})^2] (\sqrt{5x+6}-\sqrt{3x-2})^2=[(\sqrt{5x+6})^2-2\sqrt{(5x+6)(3x-2)}+(\sqrt{3x-2})^2]](/latexrender/pictures/eb56b654469ce569bca8788366c1f51b.png)



 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , mas negativo pois tem de ser no quarto quadrante. Se
, mas negativo pois tem de ser no quarto quadrante. Se  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.