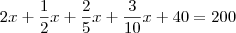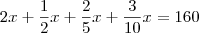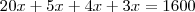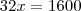por hevhoram » Seg Mai 09, 2011 17:23
tow empacado nessa questao :
O dobro da minha idade, aumentada de 1/2, dos 2/5, dos 3/10 dela e de 40 anos, resulta 200 anos. Achar minha idade.
R: 50 anos
eu comecei assim 2x + 1/2 . 2/5 .3/10 + 40 = 200 ,, mas nao deu certo como proceder??/
-
hevhoram
- Usuário Parceiro
-
- Mensagens: 61
- Registrado em: Qua Jun 02, 2010 11:43
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: informática educacional
- Andamento: formado
por FilipeCaceres » Seg Mai 09, 2011 21:00
O problema que foi fez
de
... e o enunciado quiz dizer
da idade,
da idade
Assim temos,
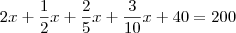
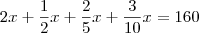
Mulitplicando tudo por 10, temos
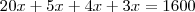
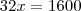
Portanto,
Abraço.
-
FilipeCaceres
- Colaborador Voluntário
-
- Mensagens: 351
- Registrado em: Dom Out 31, 2010 21:43
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Tec. Mecatrônica
- Andamento: formado
por hevhoram » Ter Mai 10, 2011 14:03
obrigado ...
-
hevhoram
- Usuário Parceiro
-
- Mensagens: 61
- Registrado em: Qua Jun 02, 2010 11:43
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: informática educacional
- Andamento: formado
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Ajuda com questão envolvendo fração
por Jovilaco » Dom Mar 24, 2013 19:15
- 3 Respostas
- 2764 Exibições
- Última mensagem por DanielFerreira
Sex Mar 29, 2013 01:04
Inequações
-
- Idade
por Ananda » Qua Fev 27, 2008 16:18
- 3 Respostas
- 3495 Exibições
- Última mensagem por admin
Qua Fev 27, 2008 18:21
Problemas do Cotidiano
-
- Idade!
por geriane » Seg Abr 05, 2010 10:49
- 3 Respostas
- 5124 Exibições
- Última mensagem por geriane
Seg Abr 05, 2010 23:57
Desafios Fáceis
-
- Idade do escritor
por Cleyson007 » Qua Jun 10, 2009 09:47
- 6 Respostas
- 3827 Exibições
- Última mensagem por ginrj
Qua Jun 10, 2009 18:04
Álgebra Elementar
-
- qual a idade?
por Claulopes » Sex Set 24, 2010 01:41
- 2 Respostas
- 3151 Exibições
- Última mensagem por Claulopes
Sex Set 24, 2010 22:56
Tópicos sem Interação (leia as regras)
Usuários navegando neste fórum: Nenhum usuário registrado e 43 visitantes
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
