a) S = { (x1, x2, x3, x4): x1 = - 2x4, x3 - 2x2 = 0 }
(i) Provar que 0 está em S, onde "0" representa o elemento neutro do espaço vetorial em questão, que nesse caso é

.
Sabemos que o 0 do espaço vetorial em questão é (0, 0, 0, 0). Ou seja,

.
Pergunta: podemos afirmar que

e
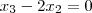
?
(ii) Provar que se u e v estão em S, então u+v também está em S.
Seja
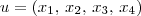
e

. Como por hipótese eles estão em S, então sabemos que:
(1)

e
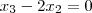
.
(2)

e
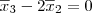
.
Por outro lado, sabemos que

.
Pergunta: considerando as afirmações (1) e (2), podemos afirmar que

e
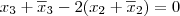
?
(iii) Provar que se u está em S e k está em R, então ku também está em S.
Seja
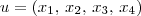
. Como por hipótese ele está em S, então sabemos que:
(1)

e
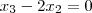
.
Por outro lado, sabemos que

.
Pergunta: considerando a afirmação (1), podemos afirmar que

e

?
Se a resposta para as três perguntas for
sim, então S é subespaço de

.
b) T = L { (1,1,0,0), (1,-1,0,2), (0,2,0,-2) }
Para resolver o exercício b) use um esquema parecido com o que foi usado para o exercício a).


 .
. .
. e
e 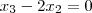 ?
?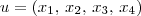 e
e  . Como por hipótese eles estão em S, então sabemos que:
. Como por hipótese eles estão em S, então sabemos que: e
e 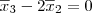 .
. .
. e
e 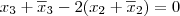 ?
? .
. e
e  ?
?
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)

 , ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
 da seguinte forma:
da seguinte forma: .
. da seguinte forma:
da seguinte forma: .
.