 por stanley tiago » Qua Abr 20, 2011 16:12
por stanley tiago » Qua Abr 20, 2011 16:12
considere a funçao

Sabendo que

,
diga quanto vale o produto abc
eu acho q é assim q deselvolve isso ;
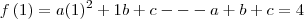
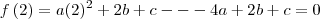
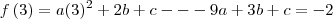
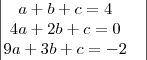
mas apartir daqui nao saiu mais nada !
-
stanley tiago
- Usuário Parceiro

-
- Mensagens: 57
- Registrado em: Seg Jan 17, 2011 14:23
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por NMiguel » Qua Abr 20, 2011 19:49
por NMiguel » Qua Abr 20, 2011 19:49
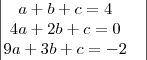
fazendo L1 <- L1-L2 e L2 <- L2-L3

fazendo L1 <- L1-L2
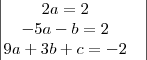
Da primeira linha da matriz obtemos a=1;
Da segunda linha e de a=1 obtemos b=-7;
Da terceira linha, de a=1 e de b=-7 obtemos c=10;
-
NMiguel
- Usuário Dedicado

-
- Mensagens: 34
- Registrado em: Ter Abr 19, 2011 17:09
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: formado
-
 por stanley tiago » Qua Abr 20, 2011 22:05
por stanley tiago » Qua Abr 20, 2011 22:05
desculpa eu acho q te confundi esse exercicio é de função do 2° grau e não de matriz
considere a funçao

Sabendo que

,
diga quanto vale o produto abc
-
stanley tiago
- Usuário Parceiro

-
- Mensagens: 57
- Registrado em: Seg Jan 17, 2011 14:23
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por NMiguel » Qui Abr 21, 2011 10:53
por NMiguel » Qui Abr 21, 2011 10:53
Não me confundiste. Eu simplesmente peguei no sistema de 3 equações que colocaste e resolvi-o da forma matricial. Qualquer matriz representa um sistema de equações lineares e qualquer sistema de equações lineares pode ser escrito como uma matriz.
Quando eu obtive a=1, b=-7 e c=10, isto significa que a tua função do segundo grau é
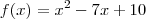
.
Assim, a resposta à tua pergunta, "quanto vale o produto abc", é -70.
-
NMiguel
- Usuário Dedicado

-
- Mensagens: 34
- Registrado em: Ter Abr 19, 2011 17:09
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: formado
-
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Função quadrática
por Ananda » Sex Mar 28, 2008 16:00
- 6 Respostas
- 9218 Exibições
- Última mensagem por admin

Sex Mar 28, 2008 21:25
Funções
-
- Função quadratica
por Aline » Qui Jun 18, 2009 14:22
- 2 Respostas
- 2621 Exibições
- Última mensagem por Cleyson007

Sex Jun 19, 2009 10:00
Funções
-
- Função Quadratica
por Aline » Qui Jun 18, 2009 14:37
- 1 Respostas
- 2006 Exibições
- Última mensagem por Marcampucio

Qui Jun 18, 2009 16:45
Funções
-
- Função Quadratica
por Aline » Sáb Jun 20, 2009 18:23
- 1 Respostas
- 2082 Exibições
- Última mensagem por Molina

Dom Jun 21, 2009 20:28
Funções
-
- Função Quadratica
 por guijermous » Sáb Abr 10, 2010 10:02
por guijermous » Sáb Abr 10, 2010 10:02
- 4 Respostas
- 8026 Exibições
- Última mensagem por Molina

Sáb Abr 10, 2010 16:27
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
[calculo] derivada
Autor:
beel - Seg Out 24, 2011 16:59
Para derivar a função
(16-2x)(21-x).x
como é melhor fazer?
derivar primeiro sei la, ((16-2x)(21-x))' achar o resultado (y)
e depois achar (y.x)' ?
Assunto:
[calculo] derivada
Autor:
MarceloFantini - Seg Out 24, 2011 17:15
Você poderia fazer a distributiva e derivar como um polinômio comum.
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:26
Funciona da mesma forma que derivada de x.y.z, ou seja, x'.y.z+x.y'.z+x.y.z' substitui cada expressão pelas variáveis e x',y' e z' é derivada de cada um
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:31
derivada de (16-2x)=-2
derivada de (21-x)=-1
derivada de x=1
derivada de (16-2x)(21-x)x=-2.(21-x)x+(-1).(16-2x)x +1.(16-2x)(21-x)
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.

 ,
,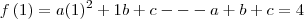
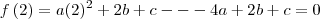
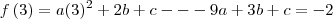
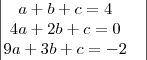 mas apartir daqui nao saiu mais nada !
mas apartir daqui nao saiu mais nada !

 ,
,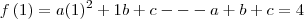
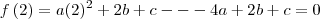
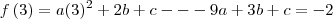
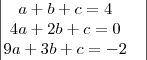 mas apartir daqui nao saiu mais nada !
mas apartir daqui nao saiu mais nada !
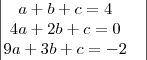

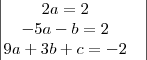


 ,
,
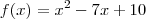 .
.