 por Molina » Ter Mar 29, 2011 20:50
por Molina » Ter Mar 29, 2011 20:50
Boa noite, Du.
Você está se confundindo nesta parte, veja:
Du21 escreveu: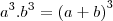
Na verdade, temos que:

Daí fecha certinho.
Bom estudo,

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por Du21 » Ter Mar 29, 2011 21:02
por Du21 » Ter Mar 29, 2011 21:02
poxa que erro idiota!

valeu pela dica Molina, consegui terminar
abração cara
-
Du21
- Novo Usuário

-
- Mensagens: 6
- Registrado em: Sex Mar 04, 2011 20:19
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Andamento: formado
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Produtos Notáveis
por Pri Ferreira » Qua Mai 23, 2012 00:10
- 0 Respostas
- 1103 Exibições
- Última mensagem por Pri Ferreira

Qua Mai 23, 2012 00:10
Álgebra Elementar
-
- Produtos notáveis e fatoração
por manuoliveira » Dom Mai 02, 2010 14:53
- 3 Respostas
- 3633 Exibições
- Última mensagem por Molina

Dom Mai 02, 2010 19:43
Sistemas de Equações
-
- Produtos Notáveis - dúvida
por laura_biscaro » Ter Fev 26, 2013 11:58
- 5 Respostas
- 2499 Exibições
- Última mensagem por e8group

Ter Fev 26, 2013 21:51
Álgebra Linear
-
- (algebra)Produtos notáveis
por Man Utd » Seg Abr 15, 2013 20:42
- 7 Respostas
- 3487 Exibições
- Última mensagem por DanielFerreira

Ter Abr 16, 2013 16:58
Álgebra Elementar
-
- Problema Produtos Notáveis e Fatoração
por Diana » Qua Ago 17, 2011 22:08
- 1 Respostas
- 1819 Exibições
- Última mensagem por Caradoc

Qua Ago 17, 2011 23:12
Sistemas de Equações
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
(FGV) ... função novamente rs
Autor:
my2009 - Qua Dez 08, 2010 21:48
Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
Assunto:
(FGV) ... função novamente rs
Autor: Anonymous - Qui Dez 09, 2010 17:25
Uma função de 1º grau é dada por

.
Temos que para

,

e para

,

.

Ache o valor de

e

, monte a função e substitua

por

.
Assunto:
(FGV) ... função novamente rs
Autor:
Pinho - Qui Dez 16, 2010 13:57
my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
f(x)= 2.x
f(3)=2.3=6
f(4)=2.4=8
f(10)=2.10=20
Assunto:
(FGV) ... função novamente rs
Autor:
dagoth - Sex Dez 17, 2010 11:55
isso ai foi uma questao da FGV?
haahua to precisando trocar de faculdade.
Assunto:
(FGV) ... função novamente rs
Autor:
Thiago 86 - Qua Mar 06, 2013 23:11
Saudações!

ví suaquestão e tentei resolver, depois você conta-me se eu acertei.
Uma função de 1º grau é dada por y=3a+b
Resposta :
3a+b=6 x(4)
4a+b=8 x(-3)
12a+4b=24
-12a-3b=-24
b=0
substituindo b na 1°, ttenho que: 3a+b=6
3a+0=6
a=2
substituindo em: y=3a+b
y=30+0
y=30

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![a = 1 + \sqrt[2]{2} a = 1 + \sqrt[2]{2}](/latexrender/pictures/82c7b3326620d0291b4db2df03063170.png)
![b = 1 - \sqrt[2]{2} b = 1 - \sqrt[2]{2}](/latexrender/pictures/ee9cf37079dde84417a1fc9046f8b35b.png)
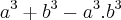 é igual a:
é igual a:![{a}^{3}.{b}^{3} = {{\left(a + b \right)}^{3} \Rightarrow \left(1 + \sqrt[2]{2} + 1 - \sqrt[2]{2}\right)}^{3} \Rightarrow {\left(2 \right)}^{3} \Rightarrow 8 {a}^{3}.{b}^{3} = {{\left(a + b \right)}^{3} \Rightarrow \left(1 + \sqrt[2]{2} + 1 - \sqrt[2]{2}\right)}^{3} \Rightarrow {\left(2 \right)}^{3} \Rightarrow 8](/latexrender/pictures/03178ccbfe1a6670ae2c83623012e9dd.png)
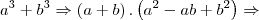
![\left(1 + \sqrt[2]{2} + 1 - \sqrt[2]{2}\right).\left[ {\left({1+\sqrt[2]{2} \right)}^{2} - \left(1+\sqrt[2]{2} \right).\left(1-\sqrt[2]{2} \right) + {\left(1-\sqrt[2]{2} \right)}^{2}\right] \Rightarrow \left(1 + \sqrt[2]{2} + 1 - \sqrt[2]{2}\right).\left[ {\left({1+\sqrt[2]{2} \right)}^{2} - \left(1+\sqrt[2]{2} \right).\left(1-\sqrt[2]{2} \right) + {\left(1-\sqrt[2]{2} \right)}^{2}\right] \Rightarrow](/latexrender/pictures/1d0542865873a8830d8cbe84035853e1.png)


![a = 1 + \sqrt[2]{2} a = 1 + \sqrt[2]{2}](/latexrender/pictures/82c7b3326620d0291b4db2df03063170.png)
![b = 1 - \sqrt[2]{2} b = 1 - \sqrt[2]{2}](/latexrender/pictures/ee9cf37079dde84417a1fc9046f8b35b.png)
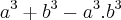 é igual a:
é igual a:![{a}^{3}.{b}^{3} = {{\left(a + b \right)}^{3} \Rightarrow \left(1 + \sqrt[2]{2} + 1 - \sqrt[2]{2}\right)}^{3} \Rightarrow {\left(2 \right)}^{3} \Rightarrow 8 {a}^{3}.{b}^{3} = {{\left(a + b \right)}^{3} \Rightarrow \left(1 + \sqrt[2]{2} + 1 - \sqrt[2]{2}\right)}^{3} \Rightarrow {\left(2 \right)}^{3} \Rightarrow 8](/latexrender/pictures/03178ccbfe1a6670ae2c83623012e9dd.png)
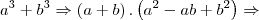
![\left(1 + \sqrt[2]{2} + 1 - \sqrt[2]{2}\right).\left[ {\left({1+\sqrt[2]{2} \right)}^{2} - \left(1+\sqrt[2]{2} \right).\left(1-\sqrt[2]{2} \right) + {\left(1-\sqrt[2]{2} \right)}^{2}\right] \Rightarrow \left(1 + \sqrt[2]{2} + 1 - \sqrt[2]{2}\right).\left[ {\left({1+\sqrt[2]{2} \right)}^{2} - \left(1+\sqrt[2]{2} \right).\left(1-\sqrt[2]{2} \right) + {\left(1-\sqrt[2]{2} \right)}^{2}\right] \Rightarrow](/latexrender/pictures/1d0542865873a8830d8cbe84035853e1.png)






 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
