 por LuizAquino » Dom Mar 20, 2011 20:37
por LuizAquino » Dom Mar 20, 2011 20:37
Abelardo escreveu:como posso saber se (
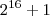
) é primo ou não?
Leia com
atenção o enunciado da questão: "Sabe-se que
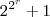
é um número primo para r= 1, 2, 3 ou 4, mas não é para 5".
Pergunta: quanto vale
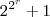
para r=4?
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- PRIMOS
por ckde » Qua Jul 14, 2010 12:20
- 11 Respostas
- 4533 Exibições
- Última mensagem por Tom

Sáb Jul 17, 2010 22:29
Álgebra Elementar
-
- Números primos
 por mony0771 » Qui Abr 23, 2009 10:54
por mony0771 » Qui Abr 23, 2009 10:54
- 2 Respostas
- 4109 Exibições
- Última mensagem por mony0771

Qui Abr 23, 2009 15:28
Álgebra Elementar
-
- Numeros Primos
por Neperiano » Sex Abr 24, 2009 20:15
- 6 Respostas
- 5729 Exibições
- Última mensagem por Neperiano

Sáb Abr 25, 2009 10:23
Problemas do Cotidiano
-
- Fatores primos
por GMAT2010 » Qua Fev 03, 2010 20:59
- 3 Respostas
- 1871 Exibições
- Última mensagem por GMAT2010

Sáb Fev 06, 2010 07:40
Funções
-
- Números Primos
por Abelardo » Qua Mar 09, 2011 21:38
- 1 Respostas
- 3060 Exibições
- Última mensagem por Abelardo

Qua Mar 09, 2011 21:41
Álgebra Elementar
Usuários navegando neste fórum: Nenhum usuário registrado e 7 visitantes
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
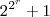 é um número primo para
é um número primo para 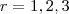 ou
ou  , mas não é para
, mas não é para  . Quantos fatores primos tem o número
. Quantos fatores primos tem o número 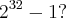
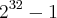 é a diferença de dois quadrados, transformei para
é a diferença de dois quadrados, transformei para 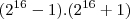 . Transformei
. Transformei  em
em 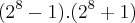 .
.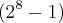 dá como resultado
dá como resultado 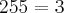 x
x x
x e
e 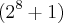 dá como resultado 257, que é primo. Logo tenho que
dá como resultado 257, que é primo. Logo tenho que  tem 4 números primos... agora fica a minha dúvida, como posso saber se
tem 4 números primos... agora fica a minha dúvida, como posso saber se  é primo ou não? (Lembrando que eu devo fazer questões dessa, futuramente, só com lápis, papel e borracha... a prova OBM)!
é primo ou não? (Lembrando que eu devo fazer questões dessa, futuramente, só com lápis, papel e borracha... a prova OBM)!

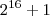 ) é primo ou não?
) é primo ou não?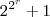 é um número primo para r= 1, 2, 3 ou 4, mas não é para 5".
é um número primo para r= 1, 2, 3 ou 4, mas não é para 5".
 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.