 por leticiamarinho_ » Dom Mar 13, 2011 14:16
por leticiamarinho_ » Dom Mar 13, 2011 14:16
Eu estava fazendo uma equação, a principio consegui fazer boa parte dela, por soma e produto, mas o problema mesmo apareceu bem no finalzinho:
A soma dos quadrados das raizes da equação x²-12+m=0 é igual a 90. O numero real de m é tal que:
RESP) m é divisivel por 9.
Bom,eu comecei fazendo uma condição de existencia, onde m é diferente de zero
depoois fiz soma e produto, onde S= 12 e P=m,
depois eu fiz o que o enunciado diz, a soma dos quadrados das raizes:
12²+m²=90
144+m²=90
m= ?54
pronto, foi ai que eu parei, raiz de 54 nao é divisivel por 9, e agora?
-
leticiamarinho_
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Dom Mar 13, 2011 13:59
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por Molina » Dom Mar 13, 2011 14:28
por Molina » Dom Mar 13, 2011 14:28
Boa tarde, Letícia.
Você está se confundindo na parte que define que S e P. Veja que realmente
S = 12 e
P = m, porém,
12 e
m não são as raízes da equação. O que você busca no artifício de Soma e Produto é realmente achar números que somados dão
12 e multiplicados dão
m. Esses números que estamos procurando é que são as raízes, que você posteriormente elevaria ao quadrado, somaria e igualaria a 90.
Minha sugestão é você fazer o desenvolvimento por Báskara desta equação. Você vai encontrar duas raízes, por exemplo,
a e
b. Daí então que você faz:

Ficou claro agora?

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por leticiamarinho_ » Dom Mar 13, 2011 14:54
por leticiamarinho_ » Dom Mar 13, 2011 14:54
Eu pensei nisso, e tentei desenvolver, mas como vou desenvolver baskara numa equação com a incognita m? simplesmente travei.
-
leticiamarinho_
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Dom Mar 13, 2011 13:59
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por Molina » Dom Mar 13, 2011 15:18
por Molina » Dom Mar 13, 2011 15:18
leticiamarinho_ escreveu:Eu pensei nisso, e tentei desenvolver, mas como vou desenvolver baskara numa equação com a incognita m? simplesmente travei.
Vamos lá:



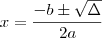
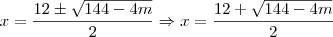
e
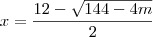
Essas são as raízes. Acredito que elevando-as ao quadrado, e depois somando, ao igualar 90 você chegará ao gabarito que m é multiplo de 9.
Caso não consiga, me informe que depois tento para você.
Bom estudo!
Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por LuizAquino » Dom Mar 13, 2011 15:20
por LuizAquino » Dom Mar 13, 2011 15:20
leticiamarinho_ escreveu: A soma dos quadrados das raízes da equação

é igual a 90. O numero real de m é tal que:
RESP) m é divisivel por 9.
A equação do exercício é essa mesma que você escreveu ou seria
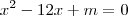
?
DicaLembre-se que
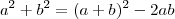
.
Editado pela última vez por
LuizAquino em Dom Mar 13, 2011 15:34, em um total de 2 vezes.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por Molina » Dom Mar 13, 2011 15:27
por Molina » Dom Mar 13, 2011 15:27
LuizAquino escreveu:leticiamarinho_ escreveu: A soma dos quadrados das raízes da equação

é igual a 90. O numero real de m é tal que:
RESP) m é divisivel por 9.
A equação do exercício é essa mesma que você escreveu ou seria
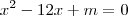
?
DicaLembre-se que
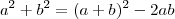
.
Bem observado, Luiz.
Mas considerei que não passou de um erro de digitação.
Vamos aguardar a confirmação dela.
Abraços.
Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por leticiamarinho_ » Seg Mar 14, 2011 14:08
por leticiamarinho_ » Seg Mar 14, 2011 14:08
Molina, consegui fazer o exercicio usando as raizes que voce me mostrou, Obrigada *-* Nem acredito que consegui, OBRIGADA
-
leticiamarinho_
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Dom Mar 13, 2011 13:59
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por LuizAquino » Seg Mar 14, 2011 14:30
por LuizAquino » Seg Mar 14, 2011 14:30
Olá leticiamarinho_,
Afinal de contas, a equação do exercício é
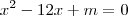
ou
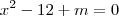
?
Em qualquer um dos casos, a forma mais simples de resolver o exercício é usando o produto notável:

.
Vejamos como ficaria para cada equação.
Equação 1:
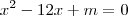
Sabemos pelos dados do exercício que:

,

e

.
Usando o produto notável indicado acima, temos que
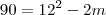
, de onde obtemos que
m = 27.
Equação 2:

Sabemos pelos dados do exercício que:

,

e

.
Novamente usando o produto notável indicado acima, temos que

, de onde obtemos que
m = -33.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Álgebra] Finalizando exercício.
por dehcalegari » Seg Mai 13, 2013 17:48
- 0 Respostas
- 1036 Exibições
- Última mensagem por dehcalegari

Seg Mai 13, 2013 17:48
Álgebra Linear
-
- equação do 2ºgrau
por jose henrique » Seg Set 13, 2010 09:26
- 5 Respostas
- 3504 Exibições
- Última mensagem por Douglasm

Dom Set 19, 2010 09:44
Álgebra Elementar
-
- Equação de 2ºgrau
por Anniinha » Dom Out 31, 2010 02:32
- 0 Respostas
- 1171 Exibições
- Última mensagem por Anniinha

Dom Out 31, 2010 02:32
Números Complexos
-
- equação do 2ºgrau
por malcionio » Dom Jun 24, 2012 11:29
- 3 Respostas
- 2361 Exibições
- Última mensagem por e8group

Dom Jun 24, 2012 18:46
Sistemas de Equações
-
- [Funções] Achar a intersecção da parábola 2ºgrau
por thoamas343 » Ter Mar 21, 2017 18:42
- 1 Respostas
- 3082 Exibições
- Última mensagem por petras

Qui Mar 23, 2017 18:28
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
zig - Sex Set 23, 2011 13:57
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
Vennom - Sex Set 23, 2011 21:41
zig escreveu:![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
Rpz, o negócio é o seguinte:
Quando você tem uma potência negativa, tu deve inverter a base dela. Por exemplo:

Então pense o seguinte: a fração geratriz de 0,05 é

, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
Veja:
![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
A raiz quadrada de vinte, você acha fácil, né?
Espero ter ajudado.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:23
Nós podemos simplificar, um pouco,

da seguinte forma:

.
É isso.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:24
Nós podemos simplificar, um pouco,

da seguinte forma:

.
É isso.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.








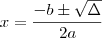
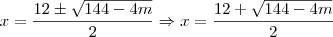 e
e 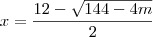
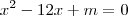 ?
?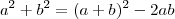 .
.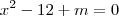 ?
? .
. ,
,  e
e  .
.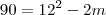 , de onde obtemos que
, de onde obtemos que  ,
,  e
e  , de onde obtemos que
, de onde obtemos que ![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)

 , ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
 da seguinte forma:
da seguinte forma: .
. da seguinte forma:
da seguinte forma: .
.