 por Jaison Werner » Qua Jan 19, 2011 09:06
por Jaison Werner » Qua Jan 19, 2011 09:06
usando os simbolos pertence e não pertence complete os espaços:
![\sqrt[]{10} \sqrt[]{10}](/latexrender/pictures/471a3f5071e0c768f7370dfae6de7f4a.png)
pertence aos Irracionais?
esta coorreto
-
Jaison Werner
- Usuário Parceiro

-
- Mensagens: 82
- Registrado em: Sex Abr 23, 2010 20:29
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em matematica
- Andamento: cursando
 por Renato_RJ » Qua Jan 19, 2011 10:51
por Renato_RJ » Qua Jan 19, 2011 10:51
Provavelmente sim, a não ser que dê uma dizima periódica muito grande....
Iniciando a minha "caminhada" pela matemática agora... Tenho muito o quê aprender...
-

Renato_RJ
- Colaborador Voluntário

-
- Mensagens: 306
- Registrado em: Qui Jan 06, 2011 15:47
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado em Matemática
- Andamento: cursando
 por VtinxD » Qua Jan 19, 2011 14:52
por VtinxD » Qua Jan 19, 2011 14:52
Na verdade ele pertence,certamente, aos irracionais.
A prova é bem simples e através da redução ao absurdo,onde se assume que
![\sqrt[]{10}\in Q \sqrt[]{10}\in Q](/latexrender/pictures/06686342582ad71fa50a2d77cea79b80.png)
e chega a uma contradição,chegando a conclusão de que ele só pode ser irracional:
Se
![\sqrt[]{10}\in Q \sqrt[]{10}\in Q](/latexrender/pictures/06686342582ad71fa50a2d77cea79b80.png)
,então:
Para

e

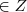
e mdc(a;b)=1
![\sqrt[]{10}=\frac{a}{b}\Rightarrow {\sqrt[]{10}}^{2}={\frac{a}{b}}^{2}\Rightarrow 10=\frac{{a}^{2}}{{b}^{2}}\Rightarrow \sqrt[]{10}=\frac{a}{b}\Rightarrow {\sqrt[]{10}}^{2}={\frac{a}{b}}^{2}\Rightarrow 10=\frac{{a}^{2}}{{b}^{2}}\Rightarrow](/latexrender/pictures/55356a00c0720f498776303c7898cae3.png)

.Que implica que

é par e multiplo de 5, por consequência

também é par e multiplo de cinco,visto que

e

pertencem aos inteiros e

diferente de zero.Se

é par então pode ser represantado por
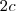
,logo:
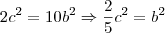
.Como

é multipo de 5 ,

também é , e como

também é inteiro,

é par que é um absurdo visto que mdc entre

e

é igual a 1.
Espero ter feito uma prova clara e ajudado a esclarecer ,adoraria outras sugestões de prova.
P.S.:Eu sei que é mais fácil com congruência modular.
-
VtinxD
- Usuário Parceiro

-
- Mensagens: 64
- Registrado em: Dom Ago 15, 2010 18:29
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Bacharelado em Matematica
- Andamento: cursando
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Conjuntos] Confusão em teoria dos conjuntos numa questão.
 por Debora Bruna » Seg Jan 11, 2016 17:44
por Debora Bruna » Seg Jan 11, 2016 17:44
- 1 Respostas
- 8837 Exibições
- Última mensagem por DanielFerreira

Sáb Jan 23, 2016 16:44
Conjuntos
-
- [Conjuntos] Dúvida sobre conjuntos vazios
por ALPC » Qui Set 18, 2014 18:28
- 5 Respostas
- 6408 Exibições
- Última mensagem por adauto martins

Seg Set 22, 2014 15:44
Conjuntos
-
- [conjuntos]numeros racionais e conjuntos
por fenixxx » Ter Fev 28, 2012 21:35
- 3 Respostas
- 4721 Exibições
- Última mensagem por DanielFerreira

Sex Mar 02, 2012 00:04
Álgebra Elementar
-
- [Conjuntos] Problema de conjuntos com porcentagem
por Tibes » Qui Jan 31, 2013 14:29
- 1 Respostas
- 7952 Exibições
- Última mensagem por young_jedi

Sex Fev 01, 2013 12:39
Conjuntos
-
- [Conjuntos] Conjuntos e geometria plana
por bencz » Dom Mar 03, 2013 12:58
- 3 Respostas
- 11197 Exibições
- Última mensagem por maison_souza

Sex Nov 14, 2014 13:15
Álgebra Elementar
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Thassya - Sáb Out 01, 2011 16:20
1) Para que os pontos (1,3) e (-3,1) pertençam ao grafico da função f(X)=ax + b ,o valor de b-a deve ser ?
2)Qual o maior valor assumido pela função f : [-7 ,10] em R definida por f(x) = x ao quadrado - 5x + 9?
3) A função f, do primeiro grau, é definida pos f(x)= 3x + k para que o gráfico de f corte o eixo das ordenadas no ponto de ordenada 5 é?
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Neperiano - Sáb Out 01, 2011 19:46
Ola
Qual as suas dúvidas?
O que você não está conseguindo fazer?
Nos mostre para podermos ajudar
Atenciosamente
Assunto:
[Função] do primeiro grau e quadratica
Autor:
joaofonseca - Sáb Out 01, 2011 20:15
1)Dados dois pontos A=(1,3) e B=(-3,1) de uma reta, é possivel definir a sua equação.


Em

substitui-se
m, substitui-se
y e
x por um dos pares ordenados, e resolve-se em ordem a
b.

2)Na equação

não existem zeros.Senão vejamos
Completando o quadrado,

As coordenadas do vertice da parabola são

O eixo de simetria é a reta

.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
f(-7)=93
f(10)=59
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![\sqrt[]{10} \sqrt[]{10}](/latexrender/pictures/471a3f5071e0c768f7370dfae6de7f4a.png) pertence aos Irracionais?
pertence aos Irracionais?
![\sqrt[]{10} \sqrt[]{10}](/latexrender/pictures/471a3f5071e0c768f7370dfae6de7f4a.png) pertence aos Irracionais?
pertence aos Irracionais?

![\sqrt[]{10}\in Q \sqrt[]{10}\in Q](/latexrender/pictures/06686342582ad71fa50a2d77cea79b80.png) e chega a uma contradição,chegando a conclusão de que ele só pode ser irracional:
e chega a uma contradição,chegando a conclusão de que ele só pode ser irracional:![\sqrt[]{10}\in Q \sqrt[]{10}\in Q](/latexrender/pictures/06686342582ad71fa50a2d77cea79b80.png) ,então:
,então: e
e 
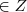 e mdc(a;b)=1
e mdc(a;b)=1![\sqrt[]{10}=\frac{a}{b}\Rightarrow {\sqrt[]{10}}^{2}={\frac{a}{b}}^{2}\Rightarrow 10=\frac{{a}^{2}}{{b}^{2}}\Rightarrow \sqrt[]{10}=\frac{a}{b}\Rightarrow {\sqrt[]{10}}^{2}={\frac{a}{b}}^{2}\Rightarrow 10=\frac{{a}^{2}}{{b}^{2}}\Rightarrow](/latexrender/pictures/55356a00c0720f498776303c7898cae3.png)
 .Que implica que
.Que implica que  é par e multiplo de 5, por consequência
é par e multiplo de 5, por consequência  também é par e multiplo de cinco,visto que
também é par e multiplo de cinco,visto que  e
e  pertencem aos inteiros e
pertencem aos inteiros e  diferente de zero.Se
diferente de zero.Se  é par então pode ser represantado por
é par então pode ser represantado por 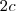 ,logo:
,logo: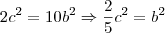 .Como
.Como  é multipo de 5 ,
é multipo de 5 , também é , e como
também é , e como  também é inteiro,
também é inteiro, é par que é um absurdo visto que mdc entre
é par que é um absurdo visto que mdc entre  e
e  é igual a 1.
é igual a 1.


 substitui-se m, substitui-se y e x por um dos pares ordenados, e resolve-se em ordem a b.
substitui-se m, substitui-se y e x por um dos pares ordenados, e resolve-se em ordem a b.
 não existem zeros.Senão vejamos
não existem zeros.Senão vejamos

 .Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.