




 parei por aqui e ñ conseguie resolver mais
parei por aqui e ñ conseguie resolver mais


 a é o numerador e b é o denominador.
a é o numerador e b é o denominador.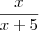
 , então:
, então: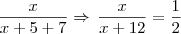
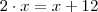
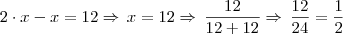

 a soma de seus termos é 34, logo
a soma de seus termos é 34, logo 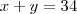 .
. , que é o sucessor de x. Então teremos:
, que é o sucessor de x. Então teremos: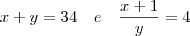
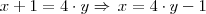
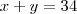 teremos:
teremos:
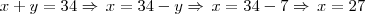


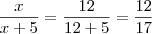


Raphael Feitas10 escreveu:Vc me ajudou muito brother agora a resposta da primeira q vc fez ta errada a resposta certa q ta aqui na apostila é 12/17,e muito obrg pela ajuda.

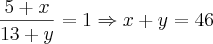




Tiago escreveu:Obrigado, valeu mesmo por resolver tbm a questão, de tão simples que ela é eu tava com dúvida.




Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.