 por Juliane » Seg Nov 22, 2010 10:32
por Juliane » Seg Nov 22, 2010 10:32
• Para transportar alimentos em seu caminhão João cobra um preço fixo de R$ 42,60 e mais R$ 0,68 por km rodado. Já o seu colega Pedro cobra uma taxa fixa de R$ 36,20 e quatro centavos a mais do que João, por km rodado. O nº de quilômetros, a partir do qual é mais barato contratar o serviço de João, é igual a:
a)160
b)162
c)164
d)166
e)168
Sei que é possível encontar o resultado testando as opções, mas acredito que há uma forma mais prática...
-
Juliane
- Usuário Ativo

-
- Mensagens: 12
- Registrado em: Sáb Set 04, 2010 17:29
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Edificações
- Andamento: cursando
 por Neperiano » Seg Nov 22, 2010 13:20
por Neperiano » Seg Nov 22, 2010 13:20
Ola
Tem sim, basta igualar as duas equações
36,20 +0,72x = 42,6 + 0,68 x
O resultado dara o valor em que os dois cobrarão igual
Atenciosamente
Sómente os mortos conhecem o fim da guerra
"Platão"
-

Neperiano
- Colaborador Voluntário

-
- Mensagens: 960
- Registrado em: Seg Jun 16, 2008 17:09
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de Produção
- Andamento: cursando
 por alexandre32100 » Seg Nov 22, 2010 13:38
por alexandre32100 » Seg Nov 22, 2010 13:38
Preço do João:

Preço do Pedro:
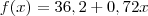
Onde

é o preço e

o número de Km rodados.

-
alexandre32100
-
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Proporção
por Roberta » Ter Jul 14, 2009 17:22
- 2 Respostas
- 3153 Exibições
- Última mensagem por Roberta

Ter Jul 14, 2009 19:53
Desafios Enviados
-
- PROPORÇÃO
por patriciagarciapoa » Qui Nov 05, 2009 16:37
- 1 Respostas
- 1770 Exibições
- Última mensagem por Lucio Carvalho

Qui Nov 05, 2009 17:14
Matemática Financeira
-
- Proporção
por Cristina Alves » Qui Fev 03, 2011 21:54
- 2 Respostas
- 2875 Exibições
- Última mensagem por Cristina Alves

Sex Fev 04, 2011 13:41
Álgebra Elementar
-
- Proporção 12
por Raphael Feitas10 » Sex Fev 18, 2011 00:06
- 1 Respostas
- 1439 Exibições
- Última mensagem por Molina

Sex Fev 18, 2011 13:29
Funções
-
- Proporção 52
por Raphael Feitas10 » Qui Mai 26, 2011 20:02
- 2 Respostas
- 1776 Exibições
- Última mensagem por Raphael Feitas10

Qui Mai 26, 2011 22:45
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
função demanda
Autor:
ssousa3 - Dom Abr 03, 2011 20:55
alguém poderia me ajudar nesse exercício aqui Uma loja de CDs adquire cada unidade por R$20,00 e a revende por R$30,00. Nestas condições,
a quantidade mensal que consegue vender é 500 unidades. O proprietário estima que, reduzindo o preço para R$28,00, conseguirá vender 600 unidades por mês.
a) Obtenha a função demanda, supondo ser linear
Eu faço ensino médio mas compro apostilas de concursos para me preparar para mercado de trabalho e estudar sozinho não é fácil. Se alguém puder me ajudar aqui fico grato
Assunto:
função demanda
Autor:
ssousa3 - Seg Abr 04, 2011 14:30
Gente alguém por favor me ensine a calcular a fórmula da função demanda

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.




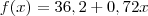
 é o preço e
é o preço e  o número de Km rodados.
o número de Km rodados.
