


a)Escreva uma equação do segundo grau, na forma ax²+bx+c=0, com a, b e
c inteiros, e que tenha raízes -2/3 e 4/5.
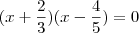
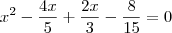

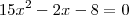












Cara Renatinha, se é que esse é mesmo o seu nome.
Não perca seu tempo tentando adivinhar quem sou, pois ao contrário de muitos, escrevo aqui o meu verdadeiro nome RICARDO ORPINELLI. Sou da área sim, formado em Matemática (bacharelado) pela Federal Fluminense (UFRJ) e pós graduado em Educação Matemática pela UNESP-Rio Claro. Apesar de não necessitar aqui decorrer sobre minha vida acadêmica.
Direcione o seu tempo em preencher as lacunas que a sua fraca graduação lhe proporcionou. Como por exemplo tentar resolver seus exercícios de "pós graduação(?)" e ai sim postar aqui suas duvidas, e não se esqueça, no seu curso da REDEFOR vc irá fazer uma avaliação sobre tudo isso que vc anda copiando daqui e ai minha querida, sinto muito lhe informar, mas não vai ter fórum no dia da prova.
Conselho: VAI ESTUDAR!!




MarceloFantini escreveu:Então acredito que você se indignará com o fórum inteiro, pois posso afirmar que em quase 100% dos casos essa regra não é seguida (infelizmente). Eu concordo com a sua crítica, apenas acho que a maneira como a colocou é muito ofensiva e desrespeitosa.

Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante


 , avisa que eu resolvo.
, avisa que eu resolvo.

