 por fttofolo » Sex Nov 19, 2010 11:05
por fttofolo » Sex Nov 19, 2010 11:05
prove que
![\sqrt[3]{2+\sqrt[2]{5}}+\sqrt[3]{2-\sqrt[2]{5}}=1 \sqrt[3]{2+\sqrt[2]{5}}+\sqrt[3]{2-\sqrt[2]{5}}=1](/latexrender/pictures/c1b67342a01ff8ef2ee26a2e4aa90a75.png)
-
fttofolo
- Usuário Dedicado

-
- Mensagens: 26
- Registrado em: Sex Nov 19, 2010 10:15
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por alexandre32100 » Sex Nov 19, 2010 13:18
por alexandre32100 » Sex Nov 19, 2010 13:18
![\sqrt[3]{2+\sqrt{5}}+\sqrt[3]{2-\sqrt{5}} \text{ (HI)} \sqrt[3]{2+\sqrt{5}}+\sqrt[3]{2-\sqrt{5}} \text{ (HI)}](/latexrender/pictures/91f20857c23163d36edb2002d843de19.png)
Se elevarmos as duas expressões ao cubo temos:
![\left ( \sqrt[3]{2+\sqrt{5}}+\sqrt[3]{2-\sqrt{5}}\right )^3=1^3=1 \left ( \sqrt[3]{2+\sqrt{5}}+\sqrt[3]{2-\sqrt{5}}\right )^3=1^3=1](/latexrender/pictures/a150e09712eb83b51a7b32a12460efcb.png)
É bom lembrar que
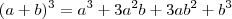
.
Aplicando isso à equação do problema:
![\\2+\sqrt{5}+3\cdot\sqrt[3]{(2+\sqrt{5})(2+\sqrt{5})(2-\sqrt{5})}+3\cdot\sqrt[3]{(2+\sqrt{5})(2-\sqrt{5})(2-\sqrt{5})}+2-\sqrt{5} \\2+\sqrt{5}+3\cdot\sqrt[3]{(2+\sqrt{5})(2+\sqrt{5})(2-\sqrt{5})}+3\cdot\sqrt[3]{(2+\sqrt{5})(2-\sqrt{5})(2-\sqrt{5})}+2-\sqrt{5}](/latexrender/pictures/df85e2bfa13d79b2e394027c3f5c51f5.png)
![\text{Obs: } (2+\sqrt{5})(2-\sqrt{5})=2^2-5=-1 \text{ e }\sqrt[3]{-1}=-1 \text{Obs: } (2+\sqrt{5})(2-\sqrt{5})=2^2-5=-1 \text{ e }\sqrt[3]{-1}=-1](/latexrender/pictures/24ade9849a5c6a358ec8ebb6d2d859cd.png)
, assim:
![4+3\cdot\sqrt[3]{(2+\sqrt{5})(-1)}+3\cdot\sqrt[3]{(2-\sqrt{5})(-1)}=4-3\cdot\left(\sqrt[3]{2+\sqrt{5}}+\sqrt[3]{2-\sqrt{5}}\right) 4+3\cdot\sqrt[3]{(2+\sqrt{5})(-1)}+3\cdot\sqrt[3]{(2-\sqrt{5})(-1)}=4-3\cdot\left(\sqrt[3]{2+\sqrt{5}}+\sqrt[3]{2-\sqrt{5}}\right)](/latexrender/pictures/3ad2d56054fec5cc2e822b2e30075522.png)
Pela HI,

, cqd.
-
alexandre32100
-
Voltar para Álgebra Elementar
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
Proporcionalidade
Autor:
silvia fillet - Qui Out 13, 2011 22:46
Divida o numero 35 em partes diretamente proporcionais a 4, 10 e 14. Em seguida divida o mesmo numero em partes proporcionais a 6, 15 e 21. explique por que os resultados sao iguais.
Assunto:
Proporcionalidade
Autor:
silvia fillet - Sáb Out 15, 2011 10:25
POR GENTILEZA PODEM VERIFICAR SE O MEU RACIOCINIO ESTÁ CERTO?
P1 = K.4 SUBSTITUINDO K POR 1,25 P1= 5
P2 = K.10 SUBSTITUINDO K POR 1,25 P2= 12,50
P3 = K.13 SUBSTITUINDO K POR 1,25 P3= 17,50
P1+P2+P3 = 35
K.4+K.10+K.13 = 35
28 K = 35
K= 1,25
P1 = K.6 SUBSTITUINDO K POR 0,835 P1= 5
P2 = K.15 SUBSTITUINDO K POR 0,835 P2 = 12,50
P3 = K.21 SUBSTITUINDO K POR 0,835 P3 = 17,50
K.6+K.15+K.21 = 35
42K = 35
K= 0,833
4/6 =10/15 =14/21 RAZÃO = 2/3
SERÁ QUE ESTÁ CERTO?
ALGUEM PODE ME AJUDAR A EXPLICAR MELHOR?
OBRIGADA
SILVIA
Assunto:
Proporcionalidade
Autor:
ivanfx - Dom Out 16, 2011 00:37
utilize a definição e não se baseie no exercícios resolvidos da redefor, assim você terá mais clareza, mas acredito que sua conclusão esteja correto, pois o motivo de darem o mesmo resultado é pq a razão é a mesma.
Assunto:
Proporcionalidade
Autor:
Marcos Roberto - Dom Out 16, 2011 18:24
Silvia:
Acho que o resultado é o mesmo pq as razões dos coeficientes e as razões entre os números são inversamente proporcionais.
Você conseguiu achar o dia em que caiu 15 de novembro de 1889?
Assunto:
Proporcionalidade
Autor:
deiasp - Dom Out 16, 2011 23:45
Ola pessoal
Tb. estou no redefor
O dia da semana em 15 de novembro de 1889, acredito que foi em uma sexta feira
Assunto:
Proporcionalidade
Autor:
silvia fillet - Seg Out 17, 2011 06:23
Bom dia,
Realmente foi uma sexta feira, como fazer os calculos para chegar ?
Assunto:
Proporcionalidade
Autor:
ivanfx - Seg Out 17, 2011 07:18
Para encontrar o dia que caiu 15 de novembro de 1889 você deve em primeiro lugar encontrar a quantidade de anos bissextos que houve entre 1889 à 2011, após isso dá uma verificada no ano 1900, ele não é bissexto, pois a regra diz que ano que é múltiplo de 100 e não é múltiplo de 400 não é bissexto.
Depois calcule quantos dias dão de 1889 até 2011, basta pegar a quantidade de anos e multiplicar por 365 + 1 dia a cada ano bissexto (esse resultado você calculou quando encontrou a quantidade de anos bissextos)
Pegue o resultado e divida por 7 e vai obter o resto.
obtendo o resto e partindo da data que pegou como referência conte a quantidade do resto para trás da semana.
Assunto:
Proporcionalidade
Autor:
silvia fillet - Seg Out 17, 2011 07:40
Bom dia,
Será que é assim:
2011 a 1889 são 121 anos sendo , 30 anos bissextos e 91 anos normais então temos:
30x366 = 10.980 dias
91x365 = 33.215 dias
incluindo 15/11/1889 - 31/12/1889 47 dias
33215+10980+47 = 44242 dias
44242:7 = 6320 + resto 2
è assim, nâo sei mais sair disso.
Assunto:
Proporcionalidade
Autor:
ivanfx - Seg Out 17, 2011 10:24
que tal descontar 1 dia do seu resultado, pois 1900 não é bissexto, ai seria 44241 e quando fizer a divisão o resto será 1
como etá pegando base 1/01/2011, se reparar bem 01/01/2011 sempre cai no mesmo dia que 15/01/2011, sendo assim se 01/01/2011 caiu em um sábado volte 1 dia para trás, ou seja, você está no sábado e voltando 1 dia voltará para sexta.então 15/11/1889 cairá em uma sexta
Assunto:
Proporcionalidade
Autor:
Kiwamen2903 - Seg Out 17, 2011 19:43
Boa noite, sou novo por aqui, espero poder aprender e ajudar quando possível! A minha resposta ficou assim:
De 1889 até 2001 temos 29 anos bissextos a começar por 1892 (primeiro múltiplo de 4 após 1889) e terminar por 2008 (último múltiplo de 4 antes de 2011). Vale lembrar que o ano 1900 não é bissexto, uma vez que é múltiplo de 100 mas não é múltiplo de 400.
De um ano normal para outro, se considerarmos a mesma data, eles caem em dias consecutivos da semana. Por exemplo 01/01/2011 – sábado, e 01/01/2010 – sexta.
De um ano bissexto para outro, se considerarmos a mesma data, um cai dois dias da semana depois do outro. Por exemplo 01/01/2008 (ano bissexto) – Terça – feira, e 01/01/09 – Quinta-feira.
Sendo assim, se contarmos um dia da semana de diferença para cada um dos 01/01 dos 122 anos que separam 1889 e 2011 mais os 29 dias a mais referentes aos anos bissextos entre 1889 e 2011, concluímos que são 151 dias da semana de diferença, o que na realidade nos trás: 151:7= 21x7+4, isto é, são 4 dias da semana de diferença. Logo, como 15/11/2011 cairá em uma terça-feira, 15/11/1889 caiu em uma sexta-feira.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![\sqrt[3]{2+\sqrt[2]{5}}+\sqrt[3]{2-\sqrt[2]{5}}=1 \sqrt[3]{2+\sqrt[2]{5}}+\sqrt[3]{2-\sqrt[2]{5}}=1](/latexrender/pictures/c1b67342a01ff8ef2ee26a2e4aa90a75.png)


![\sqrt[3]{2+\sqrt[2]{5}}+\sqrt[3]{2-\sqrt[2]{5}}=1 \sqrt[3]{2+\sqrt[2]{5}}+\sqrt[3]{2-\sqrt[2]{5}}=1](/latexrender/pictures/c1b67342a01ff8ef2ee26a2e4aa90a75.png)

![\sqrt[3]{2+\sqrt{5}}+\sqrt[3]{2-\sqrt{5}} \text{ (HI)} \sqrt[3]{2+\sqrt{5}}+\sqrt[3]{2-\sqrt{5}} \text{ (HI)}](/latexrender/pictures/91f20857c23163d36edb2002d843de19.png)
![\left ( \sqrt[3]{2+\sqrt{5}}+\sqrt[3]{2-\sqrt{5}}\right )^3=1^3=1 \left ( \sqrt[3]{2+\sqrt{5}}+\sqrt[3]{2-\sqrt{5}}\right )^3=1^3=1](/latexrender/pictures/a150e09712eb83b51a7b32a12460efcb.png)
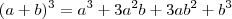 .
.![\\2+\sqrt{5}+3\cdot\sqrt[3]{(2+\sqrt{5})(2+\sqrt{5})(2-\sqrt{5})}+3\cdot\sqrt[3]{(2+\sqrt{5})(2-\sqrt{5})(2-\sqrt{5})}+2-\sqrt{5} \\2+\sqrt{5}+3\cdot\sqrt[3]{(2+\sqrt{5})(2+\sqrt{5})(2-\sqrt{5})}+3\cdot\sqrt[3]{(2+\sqrt{5})(2-\sqrt{5})(2-\sqrt{5})}+2-\sqrt{5}](/latexrender/pictures/df85e2bfa13d79b2e394027c3f5c51f5.png)
![\text{Obs: } (2+\sqrt{5})(2-\sqrt{5})=2^2-5=-1 \text{ e }\sqrt[3]{-1}=-1 \text{Obs: } (2+\sqrt{5})(2-\sqrt{5})=2^2-5=-1 \text{ e }\sqrt[3]{-1}=-1](/latexrender/pictures/24ade9849a5c6a358ec8ebb6d2d859cd.png) , assim:
, assim:![4+3\cdot\sqrt[3]{(2+\sqrt{5})(-1)}+3\cdot\sqrt[3]{(2-\sqrt{5})(-1)}=4-3\cdot\left(\sqrt[3]{2+\sqrt{5}}+\sqrt[3]{2-\sqrt{5}}\right) 4+3\cdot\sqrt[3]{(2+\sqrt{5})(-1)}+3\cdot\sqrt[3]{(2-\sqrt{5})(-1)}=4-3\cdot\left(\sqrt[3]{2+\sqrt{5}}+\sqrt[3]{2-\sqrt{5}}\right)](/latexrender/pictures/3ad2d56054fec5cc2e822b2e30075522.png)
 , cqd.
, cqd.