 por arima » Seg Nov 08, 2010 08:40
por arima » Seg Nov 08, 2010 08:40
qUEM PODE ME AJUDAR OBRIGADA: SENDO P NUMERO PRIMO PROVE QUE RAIZ DE P É RACIONAL
-
arima
- Usuário Parceiro

-
- Mensagens: 50
- Registrado em: Sáb Out 23, 2010 18:25
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Matematica
- Andamento: cursando
 por Molina » Seg Nov 08, 2010 13:42
por Molina » Seg Nov 08, 2010 13:42
arima escreveu:qUEM PODE ME AJUDAR OBRIGADA: SENDO P NUMERO PRIMO PROVE QUE RAIZ DE P É RACIONAL
Boa tarde, Arima.
Confirma o enunciado, o certo seria: SENDO P NUMERO PRIMO PROVE QUE RAIZ DE P É
IRRACIONAL
Né?!
Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por arima » Seg Nov 08, 2010 21:14
por arima » Seg Nov 08, 2010 21:14
isso mesmo provar que p é irracinal.arima
-
arima
- Usuário Parceiro

-
- Mensagens: 50
- Registrado em: Sáb Out 23, 2010 18:25
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Matematica
- Andamento: cursando
 por roseli » Seg Nov 08, 2010 22:53
por roseli » Seg Nov 08, 2010 22:53
molina escreveu:arima escreveu:qUEM PODE ME AJUDAR OBRIGADA: SENDO P NUMERO PRIMO PROVE QUE RAIZ DE P É RACIONAL
Boa tarde, Arima.
Confirma o enunciado, o certo seria: SENDO P NUMERO PRIMO PROVE QUE RAIZ DE P É
IRRACIONAL
Né?!
e daÍ Molina como fica esse exercício?
-
roseli
- Novo Usuário

-
- Mensagens: 9
- Registrado em: Seg Nov 01, 2010 22:31
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: matemática
- Andamento: cursando
 por Molina » Seg Nov 08, 2010 22:58
por Molina » Seg Nov 08, 2010 22:58
Boa noite.
Esta demonstração se prova por
absurdo. Comece supondo que

é racional (é isto que no final você vai contradizer e concluir que é irracional). Logo,

é da forma

irredutível, com

,
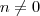
:


Logo
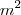
é divisível por

e consequentemente

é divisível por

.
Então, podemos escrever

, com

Com isso temos que:


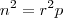
Logo

é divisível por

e consequentemente

é divisível por

.
Com isso temos um
absurdo, por assumimos inicialmente que

era irredutível, ou seja, primos entre si. E o que acabamos de mostrar que eles tem um múltiplo em comum (p).
Assim, nossa hipótese é negada e temos que

não é da forma

e com isso é IRRACIONAL.
Caso tenha dúvida em alguma passagem, informe!
Bom estudo,

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por arima » Ter Nov 09, 2010 11:50
por arima » Ter Nov 09, 2010 11:50
Valeu obrigada e tudo de bom. arima
-
arima
- Usuário Parceiro

-
- Mensagens: 50
- Registrado em: Sáb Out 23, 2010 18:25
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Matematica
- Andamento: cursando
 por roseli » Ter Nov 09, 2010 14:47
por roseli » Ter Nov 09, 2010 14:47
molina escreveu:Boa noite.
Esta demonstração se prova por
absurdo. Comece supondo que

é racional (é isto que no final você vai contradizer e concluir que é irracional). Logo,

é da forma

irredutível, com

,
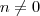
:


Logo
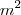
é divisível por

e consequentemente

é divisível por

.
Então, podemos escrever

, com

Com isso temos que:


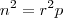
Logo

é divisível por

e consequentemente

é divisível por

.
Com isso temos um
absurdo, por assumimos inicialmente que

era irredutível, ou seja, primos entre si. E o que acabamos de mostrar que eles tem um múltiplo em comum (p).
Assim, nossa hipótese é negada e temos que

não é da forma

e com isso é IRRACIONAL.
Caso tenha dúvida em alguma passagem, informe!
Bom estudo,

Muito obrigada, tá? Bjs
-
roseli
- Novo Usuário

-
- Mensagens: 9
- Registrado em: Seg Nov 01, 2010 22:31
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: matemática
- Andamento: cursando
 por roseli » Ter Nov 09, 2010 15:51
por roseli » Ter Nov 09, 2010 15:51
arima escreveu:qUEM PODE ME AJUDAR OBRIGADA: SENDO P NUMERO PRIMO PROVE QUE RAIZ DE P É RACIONAL
Olá Arima, pelo jeito fazemos o mesmo curso: redefor.
Estou insegura sobre provar que a raiz de 3 é irracional. Pode me enviar a resposta?
E sobre os exemp da soma ou produto dos irracionais, você simplesmente pegou alguns números ou fez algo mais?
Eu ainda não respondi as questões, como foi comunicado na carta que enviaram ao cursistas.
Vou trabalhar agora, mas volto em tempo de postar. Obrigada desde já. Um abraço.
-
roseli
- Novo Usuário

-
- Mensagens: 9
- Registrado em: Seg Nov 01, 2010 22:31
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: matemática
- Andamento: cursando
 por roseli » Qua Nov 10, 2010 21:03
por roseli » Qua Nov 10, 2010 21:03
Boa noite Arima
Te mandei uma mensagem sobre o exercício anteiror, mas não me respondeu, mas tudo bem. Acabei fazendo pelo que o Molina demonstrou.
Será que poderia dividir comigo suas respostas sempre nas duas disiciplinas? Ficaria muito grata.
-
roseli
- Novo Usuário

-
- Mensagens: 9
- Registrado em: Seg Nov 01, 2010 22:31
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: matemática
- Andamento: cursando
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Demonstração
por Lorettto » Qui Dez 16, 2010 23:03
- 3 Respostas
- 2264 Exibições
- Última mensagem por Elcioschin

Seg Dez 20, 2010 12:39
Álgebra Elementar
-
- Demonstração
por Pedro2 » Sáb Mar 12, 2011 15:38
- 1 Respostas
- 1952 Exibições
- Última mensagem por Guill

Sex Abr 20, 2012 16:01
Matrizes e Determinantes
-
- PA - Demonstração
por jessicaccs » Sex Mar 25, 2011 11:52
- 1 Respostas
- 1468 Exibições
- Última mensagem por Elcioschin

Sex Mar 25, 2011 14:55
Progressões
-
- Demonstração
por tigre matematico » Dom Nov 06, 2011 12:05
- 0 Respostas
- 1074 Exibições
- Última mensagem por tigre matematico

Dom Nov 06, 2011 12:05
Funções
-
- Demonstração
por Well » Qua Mar 28, 2012 21:48
- 3 Respostas
- 1834 Exibições
- Última mensagem por LuizAquino

Qui Mar 29, 2012 12:29
Álgebra Elementar
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Exercicios de polinomios
Autor:
shaft - Qua Jun 30, 2010 17:30

Então, o exercicio pede para encontrar

.
Bom, tentei resolver a questão acima desenvolvendo as duas partes em ( )...Logo dps cheguei em um resultado q nao soube o q fazer mais.
Se vcs puderem ajudar !
Assunto:
Exercicios de polinomios
Autor:
Douglasm - Qua Jun 30, 2010 17:53
Bom, se desenvolvermos isso, encontramos:

Para que os polinômios sejam iguais, seus respectivos coeficientes devem ser iguais (ax = bx ; ax² = bx², etc.):


Somando a primeira e a segunda equação:

Finalmente:

Até a próxima.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.






 é racional (é isto que no final você vai contradizer e concluir que é irracional). Logo,
é racional (é isto que no final você vai contradizer e concluir que é irracional). Logo,  é da forma
é da forma  irredutível, com
irredutível, com  ,
, 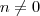 :
:

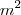 é divisível por
é divisível por  e consequentemente
e consequentemente  é divisível por
é divisível por  .
. , com
, com 


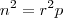
 é divisível por
é divisível por  e consequentemente
e consequentemente  é divisível por
é divisível por  .
. era irredutível, ou seja, primos entre si. E o que acabamos de mostrar que eles tem um múltiplo em comum (p).
era irredutível, ou seja, primos entre si. E o que acabamos de mostrar que eles tem um múltiplo em comum (p). não é da forma
não é da forma  e com isso é IRRACIONAL.
e com isso é IRRACIONAL.


é racional (é isto que no final você vai contradizer e concluir que é irracional). Logo,
é da forma
irredutível, com
,
:
é divisível por
e consequentemente
é divisível por
.
, com
é divisível por
e consequentemente
é divisível por
.
era irredutível, ou seja, primos entre si. E o que acabamos de mostrar que eles tem um múltiplo em comum (p).
não é da forma
e com isso é IRRACIONAL.




 .
.



