Diferentemente das outras respostas do gabarito, neste caso, a resolução tem que ser completa.
Entretanto, considerando as entre-linhas, ainda podemos questionar:
i) 1o. membro?
 ii)
ii)Soma das raízes?
 iii)
iii)Produto das raízes?
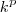
Nesta resolução, vamos evidenciar estes passos, pois provavelmente são os principais causadores de dúvidas.
Començado pelo 1o. membro, vamos reescrevê-lo em etapas para entendermos o que está no gabarito:
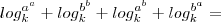





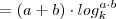
Então, o passo
(i) está mais detalhado.
Onde
a e
b são, por hipótese, as raízes da equação:

Agora, vamos percorrer a obtenção da soma e do produto das raízes de uma equação do segundo grau, para entendermos
(ii) e
(iii).
Vamos considerar esta equação, onde

,

.
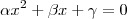
Onde as duas raízes são:
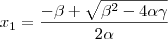
e
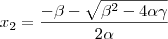
Soma das raízes:

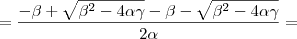
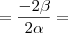

Voltando para a equação do problema:

Temos que:

e

Logo,
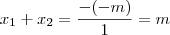
E como
a e
b são as raízes,

(passo
ii)
Produto das raízes:

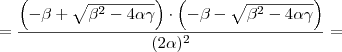

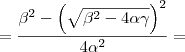
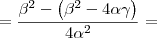
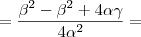

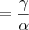
Novamente, voltando para a equação do problema:

Temos que:

,

e
a,
b são raízes.
Logo,
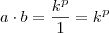
(passo
iii)
Portanto, percorremos as entre-linhas do gabarito, pois uma das maneiras para resolvermos um exercício algébrico do tipo "mostre que", é partirmos exclusivamene de um membro da equação e chegarmos ao outro, provando que são de fato iguais.
Eis um resumo do que fizemos:
Partindo do 1o. membro:
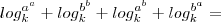

Considerando a equação:

Vimos que a soma das raízes é:

Produto das raízes:

Agora, substituíremos estes resultados na continuação do desenvolvimento do 1o. membro.
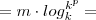

(que é o 2o. membro, onde queríamos chegar)
É claro que na prática, ou em uma resolução pessoal, nós podemos (ou, vocês podem) fazer em 4 linhas, como no gabarito.
Mas, a intenção aqui foi detalhar um pouco.
Reparem que os questionamentos podem não ter fim, como por exemplo:
-Como obtemos aquelas raízes de uma equação de segundo grau?
-Como chegamos à "fórmula de Bhaskara"?
-E as propriedades usadas de log?
-E este trecho?

Vemos que em toda resolução ficam implícitos conhecimentos prévios.





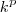
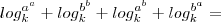





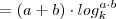

 ,
,  .
.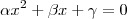
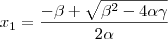
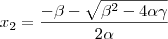

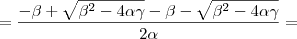
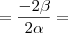

 e
e 
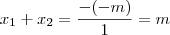
 (passo
(passo 
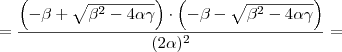

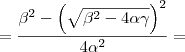
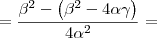
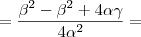

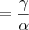
 e
e 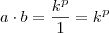 (passo
(passo 

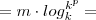

 (que é o 2o. membro, onde queríamos chegar)
(que é o 2o. membro, onde queríamos chegar) :
: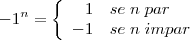
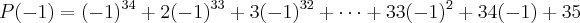



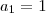 :
:

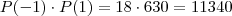





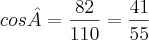

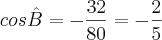


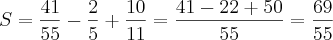

 .
.



