 por tainaraabp » Ter Out 02, 2012 11:35
por tainaraabp » Ter Out 02, 2012 11:35
limite de (?3:(x)-?3:(a))/(?5:(x²)-?5:(a²))
x tende a "a"
-
tainaraabp
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Ter Out 02, 2012 11:31
- Formação Escolar: GRADUAÇÃO
- Área/Curso: engenharia civil
- Andamento: cursando
 por LuizAquino » Ter Out 02, 2012 12:25
por LuizAquino » Ter Out 02, 2012 12:25
tainaraabp escreveu:limite de (?3:(x)-?3:(a))/(?5:(x²)-?5:(a²))
x tende a "a"
Eu presumo que o limite desejado seja o seguinte:
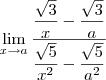
Nesse caso, note o seguinte:
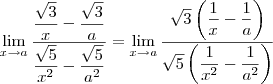
![= \lim_{x\to a} \dfrac{\sqrt{3}\left(\dfrac{1}{x} - \dfrac{1}{a}\right)}{\sqrt{5}\left[\left(\dfrac{1}{x}\right)^2 - \left(\dfrac{1}{a}\right)^2\right]} = \lim_{x\to a} \dfrac{\sqrt{3}\left(\dfrac{1}{x} - \dfrac{1}{a}\right)}{\sqrt{5}\left[\left(\dfrac{1}{x}\right)^2 - \left(\dfrac{1}{a}\right)^2\right]}](/latexrender/pictures/ac34f501eba9aee5aa8910b3a0a75d64.png)
Agora tente concluir o exercício.
ObservaçãoPara digitar as notações de modo adequado, por favor leia o tópico abaixo:
DICA: Escrevendo Fórmulas com LaTeX via BBCodeviewtopic.php?f=9&t=74
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Alguém sabe calcular essa Integral ?e?.senxdx ?
por lucat28 » Qua Mar 16, 2011 12:43
- 2 Respostas
- 2413 Exibições
- Última mensagem por lucat28

Qua Mar 16, 2011 17:35
Cálculo: Limites, Derivadas e Integrais
-
- Como resolvo essa função? ALGUÉM SABE?
por Kelvin Brayan » Qua Mai 25, 2011 13:12
- 3 Respostas
- 2754 Exibições
- Última mensagem por Kelvin Brayan

Qui Mai 26, 2011 10:58
Funções
-
- Alguém sabe como resolver????
por DMonteiro » Sáb Abr 03, 2010 23:31
- 4 Respostas
- 3650 Exibições
- Última mensagem por gambit

Ter Fev 17, 2015 00:00
Matemática Financeira
-
- Alguém sabe como resolver???
por DMonteiro » Sáb Abr 03, 2010 23:38
- 4 Respostas
- 3121 Exibições
- Última mensagem por DMonteiro

Dom Abr 04, 2010 21:40
Cálculo: Limites, Derivadas e Integrais
-
- [Equaçoes] alguem que sabe me ajude a resolver.
por teilom » Dom Ago 04, 2013 17:00
- 1 Respostas
- 1485 Exibições
- Última mensagem por DanielFerreira

Dom Ago 04, 2013 20:03
Equações
Usuários navegando neste fórum: Nenhum usuário registrado e 9 visitantes
Assunto:
(FGV) ... função novamente rs
Autor:
my2009 - Qua Dez 08, 2010 21:48
Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
Assunto:
(FGV) ... função novamente rs
Autor: Anonymous - Qui Dez 09, 2010 17:25
Uma função de 1º grau é dada por

.
Temos que para

,

e para

,

.

Ache o valor de

e

, monte a função e substitua

por

.
Assunto:
(FGV) ... função novamente rs
Autor:
Pinho - Qui Dez 16, 2010 13:57
my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
f(x)= 2.x
f(3)=2.3=6
f(4)=2.4=8
f(10)=2.10=20
Assunto:
(FGV) ... função novamente rs
Autor:
dagoth - Sex Dez 17, 2010 11:55
isso ai foi uma questao da FGV?
haahua to precisando trocar de faculdade.
Assunto:
(FGV) ... função novamente rs
Autor:
Thiago 86 - Qua Mar 06, 2013 23:11
Saudações!

ví suaquestão e tentei resolver, depois você conta-me se eu acertei.
Uma função de 1º grau é dada por y=3a+b
Resposta :
3a+b=6 x(4)
4a+b=8 x(-3)
12a+4b=24
-12a-3b=-24
b=0
substituindo b na 1°, ttenho que: 3a+b=6
3a+0=6
a=2
substituindo em: y=3a+b
y=30+0
y=30

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



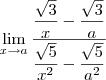
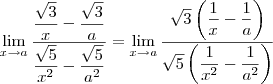
![= \lim_{x\to a} \dfrac{\sqrt{3}\left(\dfrac{1}{x} - \dfrac{1}{a}\right)}{\sqrt{5}\left[\left(\dfrac{1}{x}\right)^2 - \left(\dfrac{1}{a}\right)^2\right]} = \lim_{x\to a} \dfrac{\sqrt{3}\left(\dfrac{1}{x} - \dfrac{1}{a}\right)}{\sqrt{5}\left[\left(\dfrac{1}{x}\right)^2 - \left(\dfrac{1}{a}\right)^2\right]}](/latexrender/pictures/ac34f501eba9aee5aa8910b3a0a75d64.png)

 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
