 por aliceleite » Ter Set 04, 2012 20:20
por aliceleite » Ter Set 04, 2012 20:20
Bom, essa questão é do Programa de Avaliação Seriada da UnB, referente ao segundo ano. Eu estou com um pouco de dificuldade para resolvê-la e gostaria da ajuda de vocês.Sou nova aqui no fórum, por favor, se eu fizer algo de errado, tenham paciência comigo. Desde já, muito obrigada a todos que se prestarem a oferecer qualquer ajuda! ^^
Considere que, no esquema mostrado, a distância entre os
pontos A e B é igual a 4k, em que k é um número real positivo.
Considere, ainda, que esses pontos são simétricos em relação
à origem do sistema de coordenadas e que C = (0, -k). Com
base nesses dados, obtenha a equação da parábola que passa
pelos pontos A, B e C em função da constante k.
- Anexos
-
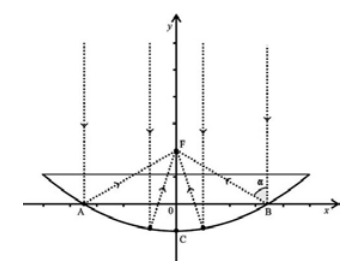
- Figura dada na prova
- Sem título.png (26.42 KiB) Exibido 1535 vezes
-
aliceleite
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Ter Set 04, 2012 20:13
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por Russman » Qua Set 05, 2012 01:31
por Russman » Qua Set 05, 2012 01:31
Bem vindo ao fórum. As regras gerais dizem que você deve postar sua tentativa de resolução. Mas vou tentar solucioná-la para você.
A equação da parábola, em uma de suas interpretações, pode ser escrita da seguinte forma:

onde

é uma constante Real e
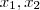
são as raízes da mesma.
Pelo gráfico vemos que os pontos

e

são as intersecções da parábola com o eixo

, isto é, suas abscissas são as raízes da equação da parábola. A saber,

e

, por exemplo.
Como a distância desses pontos é
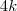
, isto é,

, pois

e
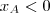
portanto

, e , como são simétricos, isto é,

, temos o seguinte sistema:

cuja solução é

e

.
Logo, adiantando a equação, temos

.
Ainda, é fato que o ponto

pertence a essa parábola. Assim,
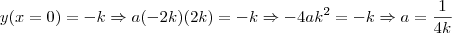
, uma vez que
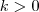
.
Portanto, a equação da parábola é

. Ou então,

.
Rigth? (:
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Parábola]Determinar vértice de parábola (Urgente!)
por migvas99 » Seg Out 08, 2012 14:37
- 1 Respostas
- 2849 Exibições
- Última mensagem por young_jedi

Seg Out 08, 2012 17:09
Funções
-
- Equação da parábola
por carolina camargo » Dom Nov 22, 2009 13:12
- 2 Respostas
- 4797 Exibições
- Última mensagem por carolina camargo

Dom Nov 22, 2009 14:18
Geometria Analítica
-
- Equação de uma parábola
por Gabi 15 » Seg Nov 14, 2011 11:24
- 3 Respostas
- 1911 Exibições
- Última mensagem por joaofonseca

Seg Nov 14, 2011 22:05
Geometria Analítica
-
- equação de uma parábola
por Ana Maria da Silva » Sex Jun 14, 2013 19:11
- 1 Respostas
- 1187 Exibições
- Última mensagem por Ana Maria da Silva

Sex Jun 21, 2013 16:03
Geometria Analítica
-
- cônicas:equação da parabola
por may » Ter Jul 12, 2011 21:35
- 2 Respostas
- 11427 Exibições
- Última mensagem por may

Sex Jul 15, 2011 00:46
Geometria Analítica
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de

Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é

Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:

Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:


Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



 é uma constante Real e
é uma constante Real e 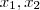 são as raízes da mesma.
são as raízes da mesma. e
e  são as intersecções da parábola com o eixo
são as intersecções da parábola com o eixo  , isto é, suas abscissas são as raízes da equação da parábola. A saber,
, isto é, suas abscissas são as raízes da equação da parábola. A saber,  e
e  , por exemplo.
, por exemplo.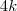 , isto é,
, isto é,  , pois
, pois  e
e 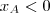 portanto
portanto  , e , como são simétricos, isto é,
, e , como são simétricos, isto é,  , temos o seguinte sistema:
, temos o seguinte sistema:
 e
e  .
. .
.  pertence a essa parábola. Assim,
pertence a essa parábola. Assim,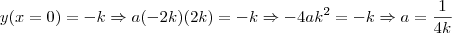 , uma vez que
, uma vez que 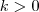 .
. . Ou então,
. Ou então,  .
.





