 por tuffy1 » Sáb Ago 25, 2012 18:35
por tuffy1 » Sáb Ago 25, 2012 18:35
Olá alguem poderia responder este exercicio eu estou com duvida e meu professor só enrola quando vou pergunta-ló.
Num triângulo retângulo um cateto mede 15cm e a hipotenusa mede 17 cm. Calcule o seno cosseno e a tangente do maior ângulo agudo desse triângulo.
Um avião levanta vôo de B e sobre fazendo um ângulo constante de 15º com a horízontal. A que altura estará e qual a distância percorrida, quando alcança a vertical que passa por uma igreja A situada a 2 km do ponto de partida?
-
tuffy1
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Sáb Ago 25, 2012 18:25
- Formação Escolar: ENSINO FUNDAMENTAL II
- Andamento: cursando
 por e8group » Sáb Ago 25, 2012 20:32
por e8group » Sáb Ago 25, 2012 20:32
Vou postar as diretrizes ,com base nisso reflita e conclua o exercício .
Considere o triângulo ABC , onde :



Ângulos agudos opostos aos segmentos |AB| e |BC|

.
Soulução :
Aplicando Teorema de Pitágoras em ABC,
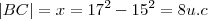
.
Utilizando relações triginometricas em ABC ,
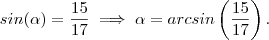

Note que
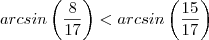
.Logo o maior
ângulo agudo é

.
Tente concluir o exercício .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por anfran1 » Dom Ago 26, 2012 10:24
por anfran1 » Dom Ago 26, 2012 10:24
Santhiago, acho que devemos simplificar a resolução de modo que o aluno entenda. Considerando que ele está do ensino fundamental, os conceitos de arcsin ainda não foram estudados e assim o menor ângulo de um triângulo é aquele que está oposto ao menor lado.
-
anfran1
- Usuário Dedicado

-
- Mensagens: 35
- Registrado em: Qui Jun 28, 2012 18:41
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por e8group » Dom Ago 26, 2012 14:04
por e8group » Dom Ago 26, 2012 14:04
anfran1 escreveu:Santhiago, acho que devemos simplificar a resolução de modo que o aluno entenda. Considerando que ele está do ensino fundamental, os conceitos de arcsin ainda não foram estudados e assim o menor ângulo de um triângulo é aquele que está oposto ao menor lado.
É ,pode ser .Minha intenção foi ajudar .Peço desculpas se o conceito acima (post anterior ) pode confundir tal aluno .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por MarceloFantini » Dom Ago 26, 2012 15:57
por MarceloFantini » Dom Ago 26, 2012 15:57
O maior ângulo agudo vê o maior cateto do triângulo. Como Santhiago já encontrou o outro cateto, basta aplicar as definições de seno, cosseno e tangente.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por tuffy1 » Dom Ago 26, 2012 18:40
por tuffy1 » Dom Ago 26, 2012 18:40
Irei responder o resto do exercício. Obrigado pelas respostas.
-
tuffy1
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Sáb Ago 25, 2012 18:25
- Formação Escolar: ENSINO FUNDAMENTAL II
- Andamento: cursando
Voltar para Trigonometria
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- exercicio proposto-triangulo retangulo
por adauto martins » Ter Out 28, 2014 10:56
- 0 Respostas
- 961 Exibições
- Última mensagem por adauto martins

Ter Out 28, 2014 10:56
Cálculo: Limites, Derivadas e Integrais
-
- [Trigonometria] Dúvida... questão sobre triangulo retangulo
 por rochadapesada » Qua Abr 24, 2013 17:57
por rochadapesada » Qua Abr 24, 2013 17:57
- 5 Respostas
- 3231 Exibições
- Última mensagem por young_jedi

Qui Abr 25, 2013 23:26
Trigonometria
-
- Calculos envolvendo triângulo retângulo e retângulo
 por andersontricordiano » Seg Abr 18, 2011 02:29
por andersontricordiano » Seg Abr 18, 2011 02:29
- 1 Respostas
- 4039 Exibições
- Última mensagem por MarceloFantini

Seg Abr 18, 2011 04:19
Progressões
-
- Dúvida em exercício {Área do triângulo}
por Danilo » Qua Jun 13, 2012 03:38
- 1 Respostas
- 1408 Exibições
- Última mensagem por LuizAquino

Qua Jun 13, 2012 11:04
Geometria Analítica
-
- Triangulo Retangulo
por ginrj » Qui Jun 04, 2009 18:56
- 1 Respostas
- 3415 Exibições
- Última mensagem por ginrj

Seg Jun 15, 2009 18:14
Geometria Plana
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.





 .
.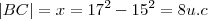 .
.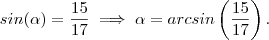

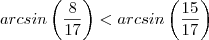 .Logo o maior
.Logo o maior  .
. 



 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.