 por -daniel15asv » Qui Ago 02, 2012 20:11
por -daniel15asv » Qui Ago 02, 2012 20:11
A diferença entre o número de lados de dois polígonos é de 3 unidades. Calcule-os, sabendo que a diferença entre o número de diagonais é de 15 unidades.
No gabarito ta pentágono e octogono .
Eu não sei como começar.
-
-daniel15asv
- Novo Usuário

-
- Mensagens: 7
- Registrado em: Qui Ago 02, 2012 19:38
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por e8group » Sex Ago 03, 2012 00:03
por e8group » Sex Ago 03, 2012 00:03
Boa noite ,
Vamos supor que o 1º polígono tem x lados e o 2° tem n lados ,com isso :

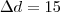
As diagonais pode ser obtidas em funções dos lados ,
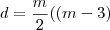
.
Assim ,
![d_2 -d_1 =15 \implies \frac{1}{2} \left[ n(n-3) -x(x-3)\right] = 15 d_2 -d_1 =15 \implies \frac{1}{2} \left[ n(n-3) -x(x-3)\right] = 15](/latexrender/pictures/129a18675abe7c2c6289b028c250dfa4.png)
.Mas ,
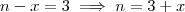
,logo
![\frac{1}{2} \left[ x(x+3 -x+3)\right] = 15 \therefore x =5 \frac{1}{2} \left[ x(x+3 -x+3)\right] = 15 \therefore x =5](/latexrender/pictures/6dfa412b267be7df6a51edb3a47af9e0.png)
,assim :

ou seja : pentágono e octógono
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por -daniel15asv » Sex Ago 03, 2012 00:24
por -daniel15asv » Sex Ago 03, 2012 00:24
Valeu Santiago muito obrigado, sua ajuda foi muito útil.
-
-daniel15asv
- Novo Usuário

-
- Mensagens: 7
- Registrado em: Qui Ago 02, 2012 19:38
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
Voltar para Geometria Plana
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Poligonos
por cristina » Qui Abr 15, 2010 19:37
- 1 Respostas
- 3249 Exibições
- Última mensagem por Elcioschin

Qui Abr 15, 2010 20:25
Geometria Plana
-
- Polígonos
por Diana » Seg Mai 23, 2011 22:10
- 4 Respostas
- 2563 Exibições
- Última mensagem por Diana

Seg Mai 23, 2011 23:19
Geometria Plana
-
- Poligonos
 por Jean Cigari » Qui Jun 30, 2011 13:50
por Jean Cigari » Qui Jun 30, 2011 13:50
- 1 Respostas
- 3805 Exibições
- Última mensagem por FilipeCaceres

Qui Jun 30, 2011 20:29
Geometria Plana
-
- poligonos com PA
por alfabeta » Qua Mar 07, 2012 20:39
- 1 Respostas
- 4236 Exibições
- Última mensagem por MarceloFantini

Qua Mar 07, 2012 23:49
Geometria Plana
-
- Polígonos não-convexos
por maria cleide » Sáb Set 24, 2011 23:03
- 1 Respostas
- 1813 Exibições
- Última mensagem por maria cleide

Qui Set 29, 2011 21:03
Geometria Plana
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Exercicios de polinomios
Autor:
shaft - Qua Jun 30, 2010 17:30

Então, o exercicio pede para encontrar

.
Bom, tentei resolver a questão acima desenvolvendo as duas partes em ( )...Logo dps cheguei em um resultado q nao soube o q fazer mais.
Se vcs puderem ajudar !
Assunto:
Exercicios de polinomios
Autor:
Douglasm - Qua Jun 30, 2010 17:53
Bom, se desenvolvermos isso, encontramos:

Para que os polinômios sejam iguais, seus respectivos coeficientes devem ser iguais (ax = bx ; ax² = bx², etc.):


Somando a primeira e a segunda equação:

Finalmente:

Até a próxima.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.




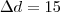
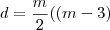 .
.![d_2 -d_1 =15 \implies \frac{1}{2} \left[ n(n-3) -x(x-3)\right] = 15 d_2 -d_1 =15 \implies \frac{1}{2} \left[ n(n-3) -x(x-3)\right] = 15](/latexrender/pictures/129a18675abe7c2c6289b028c250dfa4.png) .Mas ,
.Mas ,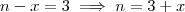 ,logo
,logo ![\frac{1}{2} \left[ x(x+3 -x+3)\right] = 15 \therefore x =5 \frac{1}{2} \left[ x(x+3 -x+3)\right] = 15 \therefore x =5](/latexrender/pictures/6dfa412b267be7df6a51edb3a47af9e0.png) ,assim :
,assim :



 .
.



