Olá pessoal! questão longa mas que não consigo fechar.
Na ilustração ao lado, temos uma garrafa de café na forma cilíndrica com altura de 20 cm e largura de 12 cm e um coador na forma cônica com 13 cm da largura por 14 cm de altura. Além do corpo cilíndrico, a garrafa tem sua parte superior no formato de tronco de cone com 6 cm de altura e perímetro da boca igual a 6? cm. Suponha que, para preparar um café, o professor Eron colocou uma mistura de pó e açúcar no coador, observando que tal mistura ocupou 1/8 do espaço do coador. Em seguida, ele acrescentou rapidamente a água quente até a borda do coador. A partir dessas informações e admitindo o valor 3 como aproximação de ?, determine:
a) A quantidade de água, em litros, que o professor Eron despejou no coador.
b) O volume, em cm³, de pó de café e açúcar colocado no coador.
c) A diferença entre o volume de água despejado no coador e o volume de uma esfera de raio igual a 5,5 cm.
d) Para lavar a garrafa de café e o coador, o professor Eron gastou um volume de água equivalente ao volume das duas peças. Assim, considerando ? = 3, determine se a quantidade de água usada pode ser colocada, sem perdas, em um recipiente semi-esférico de raio igual a 10,5 cm



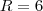 cm, pois a largura da garrafa é igual a 12 cm.
cm, pois a largura da garrafa é igual a 12 cm. cm, pois o perímetro da boca é
cm, pois o perímetro da boca é 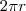 =
=  cm .
cm .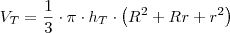 .
.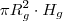 e para o cálculo do volume do cone (coador) =
e para o cálculo do volume do cone (coador) =  é aplicar tais fórmulas para os dados fornecidos e fazer os cálculos.
é aplicar tais fórmulas para os dados fornecidos e fazer os cálculos. = tronco,
= tronco,  = garrafa,
= garrafa,  = coador.
= coador.