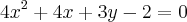
Não consegui resolver esse exercício.

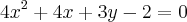


Claudin escreveu:Determine o vértice, a equação do eixo, o foco e a diretriz da parábola:
Não consegui resolver esse exercício.
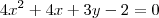
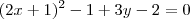
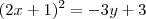



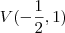

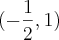 , para achar o foco
, para achar o foco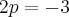

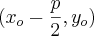
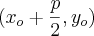
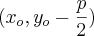


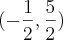





Claudin escreveu:Determine ..., o foco e a... parábola:
danjr5 escreveu:...
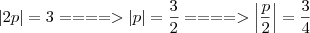
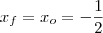
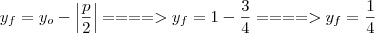
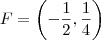
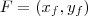 onde
onde 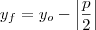 , uma vez que, o eixo de simetria é paralelo ao eixo
, uma vez que, o eixo de simetria é paralelo ao eixo  , a grosso modo,
, a grosso modo,  não varia.
não varia.
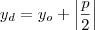
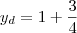
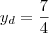
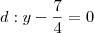

danjr5 escreveu:
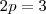
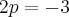 ?
?
 nao é?
nao é?

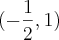

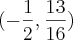
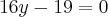

danjr5 escreveu:Claudin escreveu:Determine o vértice, a equação do eixo, o foco e a diretriz da parábola:
Não consegui resolver esse exercício.
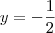
Vértice:
Portanto,
Claudin,
tente as outras, caso não consiga, retorne com as dúvidas/tentativas!!
Aguardo retorno!
Daniel F.

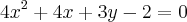
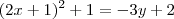
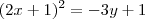

Claudin escreveu:Determine o vértice, a equação do eixo, o foco e a diretriz da parábola:
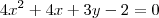
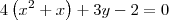
![4\left[\left(x + \frac{1}{2}\right)^2 - \frac{1}{4}\right] + 3y - 2 = 0 4\left[\left(x + \frac{1}{2}\right)^2 - \frac{1}{4}\right] + 3y - 2 = 0](/latexrender/pictures/c4cf9ad5d0ce1a8e6ec02e1ce44bf1cf.png)
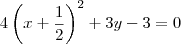
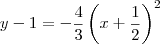
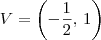 .
.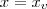 . Desse modo, temos que a equação do eixo será
. Desse modo, temos que a equação do eixo será  .
.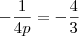
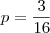
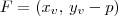 (onde
(onde 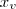 e
e  são as coordenadas x e y do vértice). Sendo assim, temos que
são as coordenadas x e y do vértice). Sendo assim, temos que 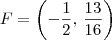 .
.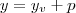 . Sendo assim, temos que a diretriz tem equação
. Sendo assim, temos que a diretriz tem equação 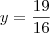 .
.
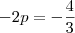


Claudin escreveu:Agora sim compreendi.
Mas a parte do Foco ainda não compreendi o porque de não ser:
No caso resultaria em
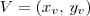 e concavidade para baixo tem o formato
e concavidade para baixo tem o formato 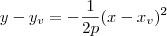 . Já se você está estudando pelo primeiro tipo, então essa mesma parábola tem equação no formato
. Já se você está estudando pelo primeiro tipo, então essa mesma parábola tem equação no formato 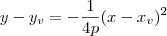 . Note que foi esse formato que usei na minha resolução.
. Note que foi esse formato que usei na minha resolução.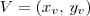 e concavidade para esquerda tem o formato
e concavidade para esquerda tem o formato 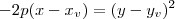 (ou simplesmente
(ou simplesmente 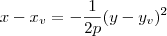 ).
).

Claudin escreveu:É, não estou entendendo pois todos exercícios de parábola que eu fiz, foram utilizando -2p
ao invés de 1/2p ou 1/4p
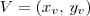 e concavidade para baixo. Em seguida, basta comparar esse formato com a equação que você obteve no exercício (que nesse caso foi
e concavidade para baixo. Em seguida, basta comparar esse formato com a equação que você obteve no exercício (que nesse caso foi 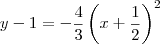 ).
).
 e
e 
 e
e 
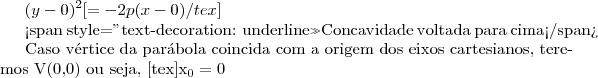 e
e 
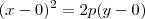
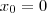 e
e 

 ou então
ou então 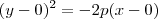


Claudin escreveu:Observei o livro e está da seguinte forma:
(...)
Concavidade voltada para baixo
Caso vértice da parábola coincida com a origem dos eixos cartesianos, teremos V(0,0) ou seja,e
fazebdo com que a equação obtida fique da seguinte forma:
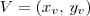 , a equação terá o formato:
, a equação terá o formato: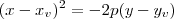
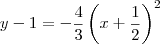
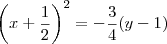
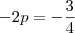 , de onde obtemos
, de onde obtemos 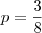 .
.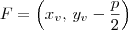 . E como temos que
. E como temos que 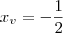 e
e  , obtemos que
, obtemos que 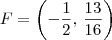 .
.Claudin escreveu:Outro problema que estou encontrando seria como diferenciar, quando é uma concavidade para esquerda, direita, cima e para baixo. Pois sabendo isso, usarei as fórmulas correspondente.
 que representa essa parábola. Isolando a variável y, obtemos que
que representa essa parábola. Isolando a variável y, obtemos que 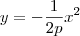 . Você já sabe que
. Você já sabe que  é sempre um número positivo. Por outro lado, p é sempre positivo por definição (consulte o seu livro). Sendo assim, o valor de
é sempre um número positivo. Por outro lado, p é sempre positivo por definição (consulte o seu livro). Sendo assim, o valor de 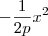 será sempre um número negativo. Ou seja, o valor de y será sempre negativo como queríamos. Perceba então como a equação da parábola é condizente com o que acontece com seu esboço.
será sempre um número negativo. Ou seja, o valor de y será sempre negativo como queríamos. Perceba então como a equação da parábola é condizente com o que acontece com seu esboço.


Voltar para Geometria Analítica
Usuários navegando neste fórum: Nenhum usuário registrado e 5 visitantes
 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , mas negativo pois tem de ser no quarto quadrante. Se
, mas negativo pois tem de ser no quarto quadrante. Se  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.