O que está errado?

[Diiim]

Boa tarde, tenho duas afirmações e não sei o que está errado, se alguém puder me ajudar...
1) Todo conjunto finito não vazio tem 1 elemento
O que está errado na seguinte demonstração: obviamente vale P(1), ou seja, temos a veracidade de C1 ou CC1
Assuma que a proposição é válida para P(n) e seja a = {x1,..., xn, xn+a}, então x1=x2=...=xn e x2=x3=...=xn=xn+1, logo x1=x2=...=xn+1 e temos a validade de P(n+1)

Não sei o que está errado!

2) O que está errado no seguinte argumento: se a diferente de 0, então a^(n-1)=1, para todo n natural

Também não sei o que está errado!
Se alguém puder me ajudar, agradeço!

[fraol]

Boa noite,

A resposta está um pouco atrasada, mas quem sabe ainda pode ajudar.

1) Todo conjunto finito não vazio tem 1 elemento

Se esse é o enunciado você pode usar um contra-exemplo para mostrar que a sentença é falsa, por exemplo: .
e A tem 5 elementos.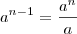

2) O que está errado no seguinte argumento: se a diferente de 0, então a^(n-1)=1, para todo n natural

, veja que a sentença não vale para muitos n ...

.