FernandaBS escreveu:Definição de limite: Seja f(x) definida num intervalo aberto I, contendo a,
exceto, possivelmente, no proprio a. Dizemos que o limite de f(X) quando x aproxima-se de a é L e escrevemos:
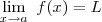
, se para todo epsilon > 0, existe um delta >0 , tal que |f(X) - L| < epsilon sempre que 0< |x-a| < delta.
Tenho dificuldade para entender o que quer dizer esse
"exceto, possivelmente, no proprio a" já que quando vou resolver um limite como por exemplo:

o que faço é justamente substituir o "x" pelo "a", que nesse caso corresponde a 1 e obtenho o limite = 2.
O que esse
"exceto, possivelmente, no proprio a" quer dizer ?? Por favor me ajudem.
Ao invés de usar a expressão "
substituir x pelo a", você não faria tanta confusão se usasse "
aproximar x por a". Os termos "
substituir" e "
aproximar" possuem uma diferença sútil.
Além disso, imagine agora que você deseja calcular

.
Perceba que você não pode aproximar x por 1 logo de início. Primeiro você precisa fazer alguma simplificação para só então fazer a aproximação.
Nesse limite, note que a função

está definida, por exemplo, em todo o intervalo aberto I = (0, 2), exceto em 1 (que é um número contido nesse intervalo).
Sendo assim, quando a definição de limite fala em "
exceto, possivelmente, no próprio a", ela está tomando cuidado com situações como essa da função f.
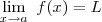 , se para todo epsilon > 0, existe um delta >0 , tal que |f(X) - L| < epsilon sempre que 0< |x-a| < delta.
, se para todo epsilon > 0, existe um delta >0 , tal que |f(X) - L| < epsilon sempre que 0< |x-a| < delta. o que faço é justamente substituir o "x" pelo "a", que nesse caso corresponde a 1 e obtenho o limite = 2.
o que faço é justamente substituir o "x" pelo "a", que nesse caso corresponde a 1 e obtenho o limite = 2.

 .
. está definida, por exemplo, em todo o intervalo aberto I = (0, 2), exceto em 1 (que é um número contido nesse intervalo).
está definida, por exemplo, em todo o intervalo aberto I = (0, 2), exceto em 1 (que é um número contido nesse intervalo).
 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.