 por lucasguilherme2 » Qui Mai 24, 2012 11:49
por lucasguilherme2 » Qui Mai 24, 2012 11:49
Prezados,
Gostaria que vocês me ajudassem no entendimento do valor do cosseno(x) e seno(x) quando X tende a infinito. Sei que o valor oscila entre 1 e -1, mas dessa conclusão não consigo tirar as respostas. Sempre fico na dúvida se é zero ou infinito ou, até mesmo, 1. Se puderem me ajudar, eu agradeço.

ass.: Lucas Guilherme
-
lucasguilherme2
- Novo Usuário

-
- Mensagens: 9
- Registrado em: Qui Mai 24, 2012 11:38
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de Materiais
- Andamento: cursando
 por LuizAquino » Qui Mai 24, 2012 19:05
por LuizAquino » Qui Mai 24, 2012 19:05
lucasguilherme2 escreveu:Gostaria que vocês me ajudassem no entendimento do valor do cosseno(x) e seno(x) quando X tende a infinito. Sei que o valor oscila entre 1 e -1, mas dessa conclusão não consigo tirar as respostas. Sempre fico na dúvida se é zero ou infinito ou, até mesmo, 1.
Cada limite é um caso. Por favor, informe o limite que você está com dificuldade.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por lucasguilherme2 » Seg Mai 28, 2012 21:51
por lucasguilherme2 » Seg Mai 28, 2012 21:51
Na verdade, é que estou estudando sequencias e,nos exercícios onde se pede a analise para ver se a função diverge ou converge, aparece a função seno e cosseno multiplicadas.
Exemplo: determinar se a seguinte função diverge ou converge.
Para isso é necessário que se faça o limite com n tendendo ao infinito, daí vem minhas dúvidas quanto ao valor do seno.
![\left[ [(2n² + 1) / (n + 1)]* sen \pi/2n \right] \left[ [(2n² + 1) / (n + 1)]* sen \pi/2n \right]](/latexrender/pictures/9b369bd52362cf222b4228d79a0bce7b.png)
![\left[ [(2n² + 1) / (n + 1)]* sen \pi/2n \right] \left[ [(2n² + 1) / (n + 1)]* sen \pi/2n \right]](/latexrender/pictures/9b369bd52362cf222b4228d79a0bce7b.png)
Se puderem me ajudar, agradeço muito.
-
lucasguilherme2
- Novo Usuário

-
- Mensagens: 9
- Registrado em: Qui Mai 24, 2012 11:38
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de Materiais
- Andamento: cursando
 por LuizAquino » Ter Mai 29, 2012 11:54
por LuizAquino » Ter Mai 29, 2012 11:54
lucasguilherme2 escreveu:Na verdade, é que estou estudando sequencias e,nos exercícios onde se pede a analise para ver se a função diverge ou converge, aparece a função seno e cosseno multiplicadas.
Exemplo: determinar se a seguinte função diverge ou converge.
Para isso é necessário que se faça o limite com n tendendo ao infinito, daí vem minhas dúvidas quanto ao valor do seno.
![\left[ [(2n² + 1) / (n + 1)]* sen \pi/2n \right] \left[ [(2n² + 1) / (n + 1)]* sen \pi/2n \right]](/latexrender/pictures/9b369bd52362cf222b4228d79a0bce7b.png)
![\left[ [(2n² + 1) / (n + 1)]* sen \pi/2n \right] \left[ [(2n² + 1) / (n + 1)]* sen \pi/2n \right]](/latexrender/pictures/9b369bd52362cf222b4228d79a0bce7b.png)
Da forma como você escreveu, a sequência seria:
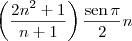
Mas ao que parece, a sequência original no exercício deve ser:
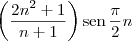
Nesse caso, você deveria ter escrito algo como:
![\left[\left(2n^2+ 1\right)/(n + 1)\right]\,\textrm{sen}\,(\pi n/2) \left[\left(2n^2+ 1\right)/(n + 1)\right]\,\textrm{sen}\,(\pi n/2)](/latexrender/pictures/5b119dd2bf8b8aba9cba187ec312bf43.png)
Perceba a importância de escrever corretamente as notações!
Feita essa observação, vejamos a resolução.
Quando
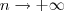
, o valor de

é indeterminado.
Dos conhecimentos de trigonometria, sabemos que:
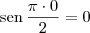






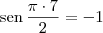

(...)
Podemos perceber nisso um padrão. Quando n é par, o valor desse seno é 0. Quando n pertence a p. a. {1, 5, 9, 13, ...}, esse valor é 1. E quando n pertence a p. a. {3, 7, 11, 15, ...}, esse valor é -1.
Sendo assim, temos que:

Perceba agora que cada parte dessa sequência tem um limite diferente quando

. A primeira parte vai para 0. Já a segunda vai para

. E a terceira vai para

.
Como cada parte tem um limite diferente, concluímos que a sequência

é divergente.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Limite com x tendendo ao infinito
por PeterHiggs » Ter Mar 04, 2014 16:53
- 2 Respostas
- 4020 Exibições
- Última mensagem por PeterHiggs

Ter Mar 04, 2014 23:08
Cálculo: Limites, Derivadas e Integrais
-
- Determinar o limite tendendo ao infinito.
por Arthur_Bulcao » Sex Mar 23, 2012 17:34
- 6 Respostas
- 5300 Exibições
- Última mensagem por Arthur_Bulcao

Qua Mar 28, 2012 19:08
Cálculo: Limites, Derivadas e Integrais
-
- (Limite) tendendo a - infinito com raiz cúbica
por kAKO » Qui Mai 07, 2015 12:18
- 1 Respostas
- 4427 Exibições
- Última mensagem por adauto martins

Sáb Mai 09, 2015 15:46
Cálculo: Limites, Derivadas e Integrais
-
- [Limite] Questão de limite tendendo à infinito
por _bruno94 » Sex Mai 31, 2013 00:28
- 3 Respostas
- 2933 Exibições
- Última mensagem por Jhonata

Sex Mai 31, 2013 01:30
Cálculo: Limites, Derivadas e Integrais
-
- [Limite] Seno e cosseno
por KleinIll » Qua Out 31, 2012 15:01
- 2 Respostas
- 2664 Exibições
- Última mensagem por e8group

Qua Out 31, 2012 20:34
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de

Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é

Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:

Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:


Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.




![\left[ [(2n² + 1) / (n + 1)]* sen \pi/2n \right] \left[ [(2n² + 1) / (n + 1)]* sen \pi/2n \right]](/latexrender/pictures/9b369bd52362cf222b4228d79a0bce7b.png)
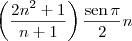
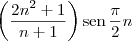
![\left[\left(2n^2+ 1\right)/(n + 1)\right]\,\textrm{sen}\,(\pi n/2) \left[\left(2n^2+ 1\right)/(n + 1)\right]\,\textrm{sen}\,(\pi n/2)](/latexrender/pictures/5b119dd2bf8b8aba9cba187ec312bf43.png)
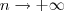 , o valor de
, o valor de  é indeterminado.
é indeterminado.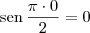






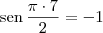


 . A primeira parte vai para 0. Já a segunda vai para
. A primeira parte vai para 0. Já a segunda vai para  . E a terceira vai para
. E a terceira vai para  .
. é divergente.
é divergente.




