Função Composta

[ginrj]

opa, galera to com dificuldade na resolução do seguinte exercicio, se alguem puder me da uma luz =]

Com base no gráfico da função y=f(x), o valor de f(f(f(1))) é?



a) -8/3
b) -5/3
c) 8/3
d) 5/3
e) 5

a resposta correta é a letra D, nao consegui entender, estou começando nessa materia agora =D, ainda tenho muitas duvidas nela ^^

[Neperiano]

Ola

É bem chatinha de resolver

Primeiro pegue f(1) = 3

Logo o proximo será f(3)=5

Depois f(5)=olhando no gráfico, mais ou menos se ve 1,66

Atenciosamente

[MarceloFantini]

Não é necessário chutar o valor, encontre a equação da reta e veja o valor quando .

[Fany Graff]

Ola galera....
Alguem poderia fazer uma resolução + "clara" da questão?
grata!

[LuizAquino]

Com base no gráfico da função y=f(x), o valor de f(f(f(1))) é?

funcaocomposta.png (7.56 KiB) Exibido 15501 vezes

a) -8/3
b) -5/3
c) 8/3
d) 5/3
e) 5

Ola galera....
Alguem poderia fazer uma resolução + "clara" da questão?

Desejamos calcular f(f(f(1))). Precisamos começar pela operação mais interna, que é f(1). Analisando o gráfico, temos que f(1)=3. Veja a figura abaixo.

funcaocomposta_f(1).png (7.63 KiB) Exibido 15501 vezes

Temos então f(f(3)) agora. A operação mais interna é f(3). Analisando o gráfico, temos que f(3) = 5. Veja a figura abaixo.

funcaocomposta_f(3).png (6.63 KiB) Exibido 15501 vezes

Temos então f(5) agora. Analisando o gráfico, não temos exatamente qual é esse valor. Veja a figura abaixo.

funcaocomposta_f(5).png (7.14 KiB) Exibido 15501 vezes

Para determinar o valor exato de f(5), devemos determinar a equação da reta que passa pelos pontos (3, 5) e (6, 0).

Sabemos que a equação da reta tem o formato y = ax + b.

Sabemos também que o ponto (3, 5) significa que x = 3 e y = 5. Já o ponto (6, 0) significa que x = 6 e y = 0.

Usando essas informações, podemos montar um sistema de equações:



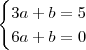
Resolvendo esse sistema, temos que e .

A equação da reta é então .

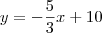
Como queremos f(5), basta substituir x por 5 na equação acima e obtemos que:



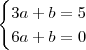
Sendo assim, temos que .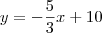