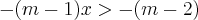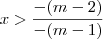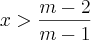por CACO » Qua Mai 02, 2012 00:17
por CACO » Qua Mai 02, 2012 00:17
ESTOU NO MEIO DE UMA INEQUAÇÃO SIMPLES MAS NÃO ENTENDO O ERRO QUE ESTOU COMETENDO. SEGUE:
(CN) Sendo m < 1 , resolva a inequação: ( x - 1 ) < x - 2.
O que tem de errado em: m(x-1)<x-2 entao mx-m<x-2 entao mx-x<m-2 entao x(m-1)<m-2 entao x<m-2/m-1?
Mas a resposta é x>m-2/m-1.
OBRIGADO!
-
CACO
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Ter Mai 01, 2012 23:49
- Formação Escolar: GRADUAÇÃO
- Área/Curso: CIÊNCIAS AERONÁUTICAS
- Andamento: formado
 por DanielFerreira » Qua Mai 02, 2012 01:03
por DanielFerreira » Qua Mai 02, 2012 01:03
Caco,
verifique se a questão está completa. Cadê o "m" na inequação??
(CN) Sendo m < 1 , resolva a inequação: ( x - 1 ) < x - 2.
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
 por CACO » Qua Mai 02, 2012 09:41
por CACO » Qua Mai 02, 2012 09:41
CORREÇÃO. FALTAVA O "m". AGORA ESTÁ COMPLETA.
(CN) Sendo m < 1 , resolva a inequação: m ( x - 1 ) < x - 2.
OBRIGADO!
-
CACO
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Ter Mai 01, 2012 23:49
- Formação Escolar: GRADUAÇÃO
- Área/Curso: CIÊNCIAS AERONÁUTICAS
- Andamento: formado
 por DanielFerreira » Qui Mai 03, 2012 21:43
por DanielFerreira » Qui Mai 03, 2012 21:43
CACO escreveu:CORREÇÃO. FALTAVA O "m". AGORA ESTÁ COMPLETA.
(CN) Sendo m < 1 , resolva a inequação: m ( x - 1 ) < x - 2.
OBRIGADO!
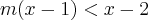

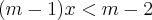
Até aqui beleza?!!
Do enunciado, temos a seguinte condição:
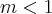
============================>
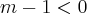
(note que esse "valor" é o mesmo que multiplica
x).
Portanto, sabemos que ele é negativo. Cabe-nos multiplicar por (- 1), como de costume!! Rsrs
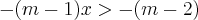
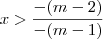
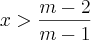
Espero ter ajudado!
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
 por CACO » Sex Mai 04, 2012 21:46
por CACO » Sex Mai 04, 2012 21:46
Agora sim, entendi. Estou (sou) enferrujado mesmo. Obrigado.
-
CACO
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Ter Mai 01, 2012 23:49
- Formação Escolar: GRADUAÇÃO
- Área/Curso: CIÊNCIAS AERONÁUTICAS
- Andamento: formado
 por DanielFerreira » Sáb Mai 05, 2012 20:53
por DanielFerreira » Sáb Mai 05, 2012 20:53
CN não é nada simples!
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
Voltar para Sistemas de Equações
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [INEQUAÇÂO] Inequação do tipo: (a+ x < b + x < c + x)
por Diofanto » Dom Fev 03, 2013 19:55
- 7 Respostas
- 6312 Exibições
- Última mensagem por Diofanto

Qui Fev 14, 2013 23:45
Inequações
-
- [inequação modular] DÚVIDA SIMPLES EM INEQUAÇÃO MODULAR
por brunocunha2008 » Sex Set 13, 2013 22:37
- 1 Respostas
- 7392 Exibições
- Última mensagem por Rafael Henrique

Qui Jan 03, 2019 14:39
Inequações
-
- Inequação
por Luna » Seg Set 28, 2009 18:55
- 4 Respostas
- 3726 Exibições
- Última mensagem por Molina

Ter Set 29, 2009 16:50
Sistemas de Equações
-
- Inequação
por Luna » Ter Set 29, 2009 16:48
- 1 Respostas
- 2114 Exibições
- Última mensagem por Molina

Qua Set 30, 2009 00:39
Sistemas de Equações
-
- Inequação
por Bebel » Dom Ago 08, 2010 00:50
- 0 Respostas
- 1623 Exibições
- Última mensagem por Bebel

Dom Ago 08, 2010 00:50
Trigonometria
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
[calculo] derivada
Autor:
beel - Seg Out 24, 2011 16:59
Para derivar a função
(16-2x)(21-x).x
como é melhor fazer?
derivar primeiro sei la, ((16-2x)(21-x))' achar o resultado (y)
e depois achar (y.x)' ?
Assunto:
[calculo] derivada
Autor:
MarceloFantini - Seg Out 24, 2011 17:15
Você poderia fazer a distributiva e derivar como um polinômio comum.
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:26
Funciona da mesma forma que derivada de x.y.z, ou seja, x'.y.z+x.y'.z+x.y.z' substitui cada expressão pelas variáveis e x',y' e z' é derivada de cada um
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:31
derivada de (16-2x)=-2
derivada de (21-x)=-1
derivada de x=1
derivada de (16-2x)(21-x)x=-2.(21-x)x+(-1).(16-2x)x +1.(16-2x)(21-x)
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



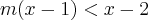

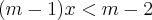
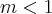 ============================>
============================> 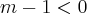 (note que esse "valor" é o mesmo que multiplica
(note que esse "valor" é o mesmo que multiplica