 por ccvenus » Qua Jun 10, 2009 23:16
por ccvenus » Qua Jun 10, 2009 23:16
Olá,
Estou com dificuldade nesse exercício da Vunesp de 1995


Em um primeiro momento tentei achar o f(x)=ax+b CD, mas como f(7) não tem imagem não consegui encontrar. Teria que tentar achar esse f(x) em função da incógnita da imagem de f(7)? Eu posso afirmar que nesse gráfico existem três funções diferentes?
Obrigada

-
ccvenus
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Qua Jun 10, 2009 22:53
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Cursinho
- Andamento: cursando
 por Molina » Qui Jun 11, 2009 02:07
por Molina » Qui Jun 11, 2009 02:07
Boa noite.
É mais ou menos isso que você está pensando. Podemos "dividir" esta função em três partes:
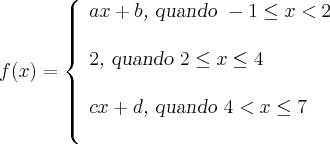
Tente a partir daqui.
Abraços!

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- (VUNESP-SP) Função
por Rafael16 » Ter Mar 13, 2012 21:11
- 3 Respostas
- 6155 Exibições
- Última mensagem por Russman

Qui Jun 21, 2012 17:13
Funções
-
- Gráfico de função trigonométrica-Função seno
 por lucassouza » Dom Mai 31, 2015 19:15
por lucassouza » Dom Mai 31, 2015 19:15
- 0 Respostas
- 1885 Exibições
- Última mensagem por lucassouza

Dom Mai 31, 2015 19:15
Trigonometria
-
- VUNESP
por DanielFerreira » Seg Fev 28, 2011 09:49
- 2 Respostas
- 8254 Exibições
- Última mensagem por DanielFerreira

Seg Fev 28, 2011 11:01
Progressões
-
- ( Vunesp )
por my2009 » Sex Jul 29, 2011 12:18
- 1 Respostas
- 1066 Exibições
- Última mensagem por Molina

Sex Jul 29, 2011 16:21
Funções
-
- grafico de função
por Amparo » Dom Mar 09, 2008 20:22
- 1 Respostas
- 2576 Exibições
- Última mensagem por admin

Qui Mar 13, 2008 12:56
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
cálculo de limites
Autor:
Hansegon - Seg Ago 25, 2008 11:29
Bom dia.
Preciso de ajuda na solução deste problema, pois só chego ao resultado de 0 sobre 0.
Obrigado
\lim_{x\rightarrow-1} x³ +1/x²-1[/tex]
Assunto:
cálculo de limites
Autor:
Molina - Seg Ago 25, 2008 13:25

Realmente se você jogar o -1 na equação dá 0 sobre 0.
Indeterminações deste tipo você pode resolver por L'Hôpital
que utiliza derivada.
Outro modo é transformar o numerador e/ou denominador
para que não continue dando indeterminado.
Dica: dividir o numerador e o denominador por algum valor é uma forma que normalmente dá certo.

Caso ainda não tenha dado uma

, avisa que eu resolvo.
Bom estudo!
Assunto:
cálculo de limites
Autor:
Guill - Dom Abr 08, 2012 16:03



Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.





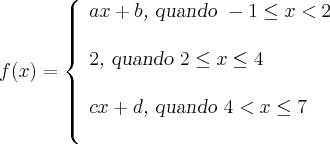



 , avisa que eu resolvo.
, avisa que eu resolvo.

